
Linguagem R

02/02/2022
Linguagem R
Em muitos estudos, sobretudo na Epidemiologia, o principal objetivo está em comparar grupos de indivíduos, com e sem uma determinada característica, em relação ao evento de interesse do pesquisador. Ao comparar um grupo com o outro, o que está sendo investigado, na verdade, é o quanto a presença ou ausência daquela característica está associada à ocorrência do evento. A característica, que na Estatística também é conhecida como covariável ou variável independente ou preditora, pode ser entendida como o fator de risco ou fator de exposição, sendo os indivíduos que apresentam o fator de risco ou de exposição classificados como expostos (e como não expostos aqueles que não o apresentam). O evento de interesse, por sua vez, é a variável dependente ou resposta, denominações mais usuais na Estatística, ou o desfecho, termo frequentemente usado na Epidemiologia, e consideraremos desfecho a partir de agora. Para efeitos práticos, vamos supor que, em uma pesquisa, deseja-se saber se uma gestante que é obesa aumenta sua chance de ter uma gestação com malformação fetal (prematura) em comparação a uma gestante que não é obesa. Nesse caso, o fator de risco é ter ou não ter excesso de gordura corporal e o desfecho é se a gravidez foi prematura ou não.
Os resultados dos cruzamentos entre essas informações poderiam ser resumidos em uma tabela de contingência 2×2, na qual, geralmente, a linha representa o fator de risco (hipertensão: sim ou não; tabagista: sim ou não; tratamento: medicação ou placebo etc) e a coluna representa o desfecho (câncer metastático: sim ou não; infarto: fatal ou não fatal; evolução: óbito ou cura etc). Definimos i, i=1,2, como a i-ésima linha, e j, j=1,2, como a j-ésima coluna. Genericamente, ela poderia ser estruturada da seguinte forma:
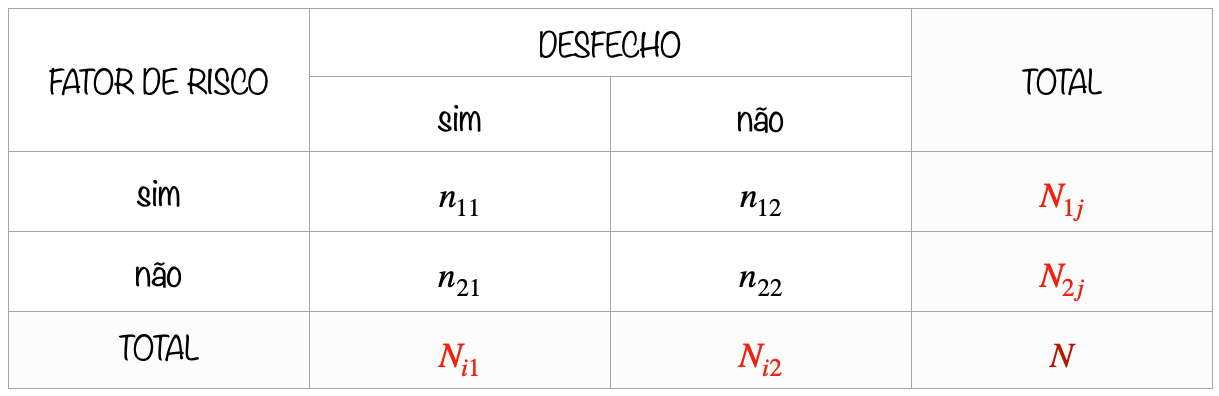
Um detalhe bastante importante e para o qual devemos chamar a atenção é que usamos a expressão “aumenta sua chance” (no exemplo das gestantes obesas) em vez de “tem maior risco”. Apesar de parecerem bastante semelhantes em termos semânticos, são expressões que devem ser usadas com muito rigor, pois estão diretamente relacionadas à medida de associação empregada.
Neste post, daremos ênfase às medidas Risco Relativo (RR) e Odds Ratio (OR), que, embora tenham a mesma finalidade de analisar a associação entre fator de risco e desfecho, possuem formas funcionais e propriedades particulares, sem contar que seu uso deve ser sempre concordante com o tipo de delineamento amostral utilizado (deixamos como sugestão de leitura o post Delineamentos de estudos aplicados à saúde, do nosso colega Pedro). Discutiremos, portanto, sobre como calcular essas medidas de maneira pontual e intervalar e algumas propriedades, deixando claras suas principais diferenças, e realizaremos computacionalmente exemplos com dados reais para melhor absorção do conteúdo aqui abordado.
Definimos como risco relativo (RR) a razão entre a incidência do desfecho no grupo dos expostos e a incidência do desfecho no grupo dos não expostos. Em primeiro lugar, algo importante a se dizer é que uma incidência significa o número de indivíduos que obtiveram respostas positivas para o desfecho de interesse no decorrer do estudo dividido pelo número total de indivíduos observados (com e sem o desfecho). Além disso, temos que o risco relativo nada mais é do que uma razão de incidências, ou seja, uma razão de probabilidades para a qual denotaremos a probabilidade de sucesso como πi. Tomando como base a tabela genérica dada na Introdução, podemos denotar algebricamente o risco relativo como sendo
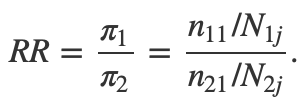
É intuitivo pensar que o resultado pode ser qualquer valor maior ou igual a zero, porém sua interpretação é diferente quando RR<1, RR=1 e RR>1. Enquanto um risco relativo menor do que 1 significa um menor risco de desenvolver o desfecho no grupo dos expostos, um risco relativo maior do que 1 quer dizer quantas vezes mais o desfecho acontece entre os expostos do que entre os não expostos. Já um risco relativo exatamente (ou muito próximo) de 1 é equivalente a dizer que o risco do desfecho ocorrer é idêntico entre os expostos e os não expostos.
Como podemos notar, o risco relativo pode ser considerado como um parâmetro a ser estimado, uma vez que está diretamente ligado a proporções amostrais. Sendo assim, podemos querer saber sobre a variabilidade encontrada da estimativa, que pode ser calculada por meio de intervalos com γ=(1−α)100% de confiança. Não entraremos em detalhes em como chegar à expressão final do intervalo de confiança para o risco relativo, mas vamos usar como referência o intervalo descrito por Gardner e Altman (1989), que consideram que os valores do risco relativo seguem uma distribuição Normal após uma transformação logarítmica. À vista disso, temos que
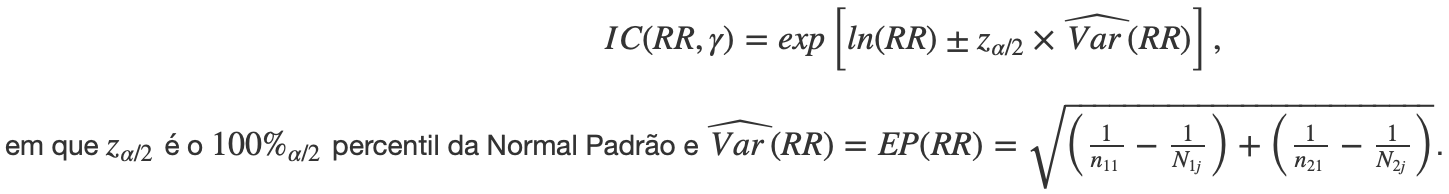
Sua interpretação é a mesma das formas usuais de intervalo de confiança e, nesse caso, só podemos inferir que existe significância estatística se o 1 não está contido no intervalo (pois RR=1 aponta para não associação entre fator de risco e desfecho).
Por último, mas longe de ser menos importante, é preciso deixar claro em qual tipo de delineamento de estudo usar a medida risco relativo é adequado. Perceba até aqui que falar em risco ou incidência sempre remete a uma ideia futura. Em outra palavras, o que queremos dizer é que cálculos de incidências e, consequentemente, de riscos relativos são exclusivos de estudos prospectivos, como os de coorte. Em estudos de coorte, por exemplo, os indivíduos expostos e não expostos ao fator de risco são acompanhados antes do desfecho de interesse ocorrer, contabilizando após um período de tempo as quantidades que manifestaram e que não manifestaram o desfecho.
Para compreender melhor todos os conceitos apresentados nesta seção, vamos utilizar o R para calcular (e interpretar) a estimativa pontual e também intervalar do risco relativo ao avaliar se uma gestante diagnosticada com diabetes gestacional que tem histórico de diabetes na família a coloca em maior risco de precisar usar insulina antes do parto em comparação a se ela não tivesse o histórico de diabetes na família. Os dados são resultantes de pesquisas realizadas entre os anos de 2012 a 2015 no Departamento de Obstetrícia da Faculdade de Medicina da Universidade de São Paulo (FM-USP), em particular pelos ambulatórios de diabetes gestacional.
A tabela de contingência para o nosso problema pode ser vista logo abaixo. Preferimos ocultar o código porque o processo até a construção da tabela, embora muito simples, não faz parte do escopo deste post – e por isso, apenas a carregamos já pronta com a função readRDS( ). Note que os totais, por linha e por coluna e também o da amostra, não aparecem na tabela gerada. Mas não se preocupe, a função responsável em calcular o risco relativo fará isso automaticamente para nós.
tabela_contingencia_rr <- readRDS("tabela.rds"); tabela_contingencia_rr

Antes de iniciar os cálculos, vale ressaltar que nesse exemplo é conveniente estimar o risco relativo porque as gestantes diagnosticadas com diabetes gestacional com e sem histórico de diabetes na família foram selecionadas antes de medicá-las (ou não) com insulina em algum momento anterior ao parto.
Para calcular o risco relativo pontual e seu intervalo, utilizaremos a função RelRisk( ), do pacote {DescTools}, que se baseia na casela n_11 como referência. No argumento x é necessário definir um vetor numérico ou uma matriz de números com dimensão 2×2, que, em nosso caso, será o objeto tabela_contigencia_rr. Como também estamos interessados no intervalo de confiança para RR, adicionaremos o argumento conf.int = .95, pois vamos calculá-lo ao nível de significância de 5%. Por fim, no argumento method devemos colocar "wald", já que queremos que os intervalos de confiança sejam calculados usando a aproximação pela distribuição Normal.
RelRisk(
x = tabela_contingencia_rr,
conf.level = .95,
method = “wald”
)
## rel. risk lwr.ci upr.ci
## 1.545904 1.125233 2.123843
Como resultado, temos que o risco relativo é aproximadamente 1,54, estimativa considerada significativa do ponto de vista intervalar (lwr.ci, o limite inferior, upr.ci, o limite superior). Por essa razão, podemos concluir que o risco de precisar usar insulina antes do parto de uma gestante diagnosticada com diabetes gestacional é 1,54 maior do que de uma gestante, sob as mesmas condições, que não tem histórico da doença na família. De outra forma, considerando o intervalo de confiança encontrado, poderíamos afirmar que o risco de uma gestante diagnosticada com diabetes gestacional e que tem histórico de diabetes na família usar insulina antes do parto é entre 1,12 e 2,12 maior do que se ela não tivesse o histórico.
Diferente de como apresentamos o risco relativo, vamos explicar sobre a odds ratio partindo de qual delineamento de estudo seu uso é pertinente. Spoiler: retrospectivo!
Em estudos retrospectivos, primeiramente identificam-se os indivíduos com e sem o desfecho de interesse no presente e depois avalia-se a exposição de cada um ao fator de risco no passado. Em especial, em estudos retrospectivos do tipo caso-controle, os indivíduos que têm o desfecho são definidos como casos e os indivíduos que não têm o desfecho, como controles. Nesse sentido, a proporção de indivíduos com e sem o desfecho depende inteiramente da quantidade de casos e controles que foram pré-selecionados pelo pesquisador, tornando cálculos de incidências e de riscos relativos inverossímeis nesse tipo de delineamento. No entanto, se observarmos bem a tabela genérica e lembrarmos de como se calcula o risco relativo, conseguimos estimar o risco relativo em um estudo de caso-controle devido o valor do RR ser razoalvemente próximo da odds ratio (OR) (ou razão de chances, em português) num cenário em que o percentual de casos é raro (Wagner & Callegari-Jacques (1998) consideram como raro um valor igual ou menor do que 10%). Mas antes de mostrar a cara matemática da odds ratio, vamos tentar entender o que é uma odds (ou chance) a princípio.
Para a probabilidade de sucesso πi dada na seção anterior, uma odds é definida como sendo
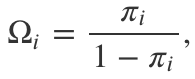
ou seja, a probabilidade de casos que foram expostos ao fator de risco divida pelo seu complementar (ou, de outro modo, pela probabilidade de controles que foram expostos ao fator de risco). Aqui, vale uma observação: apesar de uma odds ser calculada em função de probabilidades, não podemos afirmar que ela se trata de uma probabilidade propriamente dita. Logo, a odds ratio (ou razão de chances) é simplesmente uma razão entre odds, isto é,
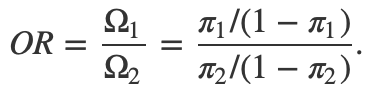
Podemos resumir a expressão acima em termos das quantidades das caselas da tabela apresentada lá no início deste exposto. Dessa forma,
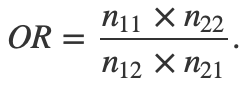
Repare que o valor de OR não muda quando invertemos a orientação da tabela de tal maneira que as linhas se tornam as colunas e as colunas se tornam as linhas.
Semelhante ao risco relativo, a odds ratio retorna um valor maior ou igual a zero e sua interpretação é feita de acordo com valores menores, iguais ou maiores do que 1. Se OR=1, ter ou não ter o fator de risco não influencia na ocorrência do desfecho. Por outro lado, se OR>1, a chance de desenvolver o desfecho é mais provável no grupo dos indivíduos que têm o fator de risco do que entre aqueles que não o têm. Entretando, se OR<1, sugere-se concluir pelo inverso do valor estimado. Para esse caso em específico, tomemos um exemplo: no artigo The Influenza Vaccine May Protect Pregnant and Postpartum Women against Severe COVID-19, no qual OR=0,33, concluiu-se que a chance de gestantes e puérperas virem a óbito por COVID-19 não recebendo a vacina é 3 vezes mais do que entre aquelas que tomaram a vacina.
Intervalos com γ=(1−α)100% de confiança também podem e devem ser calculados para a odds ratio, pois são uma forma que encontramos para atestar significância estatística para nossa estimativa. Para isso, o intervalo não pode conter o 1 pelo mesmo motivo visto pela ótica do risco relativo. Vamos usar a fórmula do intervalo de confiança para a odds ratio apresentada por Gardner & Altman (1989), que, de forma análoga ao RR, assumem que seus valores amostrais possuem distribuição Log-Normal, posteriormente normalizada pela transformação logarítmica. Assim, temos:

Agora vamos ao exemplo prático!
Dessa vez, vamos usar as bases de Síndrome Respiratória Aguda Grave (SRAG) disponibilizadas pelo DATASUS, do Ministério da Saúde, e datadas do ano 2016 a 2022. Com esse dados, a proposta é descobrir o quanto gestantes e puérperas terem sintoma de diarreia está associado à infecção por COVID-19. Lembre-se: primeiro foram selecionadas as gestantes e puérperas com e sem COVID-19 para depois separá-las no grupo das expostas (teve diarreia) e das não expostas (não teve diarreia).
A tabela de contingência para esse problema se encontra a seguir. Um adendo: consideramos como não COVID todos aqueles casos de SRAG em que o agente etiológico foi identificado como influenza, outro vírus respiratório ou outro agente etiológico.
tabela_contingencia_or <- readRDS("tabela2.rds"); tabela_contingencia_or

Para calcular as estimativas pontual e intervalar para a odds ratio, utilizaremos a função OddsRatio( ), também do pacote {DescTools}. Os argumentos para essa função serão quase os mesmos de antes, com a diferença que vamos atribuir o objeto tabela_contingencia_or no argumento x.
OddsRatio(
x = tabela_contingencia_or,
conf.level = .95,
method = “wald”
)
## odds ratio lwr.ci upr.ci
## 2.253148 1.761268 2.882399
Quanto à interpretação do resultado, podemos inferir que a chance de gestantes e puérperas confirmarem a infecção pela COVID-19 é cerca de 2,25 vezes mais tendo diarreia como sintoma do que entre aquelas que não apresentaram tal sintoma (ou, pelo intervalo de confiança: a chance de gestantes e puérperas que tiveram diarreia positivar para COVID-19 é entre 1,76 e 2,88 vezes mais a chance de gestantes e puérperas que não tiveram diarreia).
Neste post, discutimos sobre os principais conceitos de duas medidas de associação bastante importantes e aplicadas na área da saúde, o Risco Relativo e a Odds Ratio. Mostramos suas diferenças mais notáveis, principalmente no que se refere ao tipo de delineamento de estudo em que deve ser corretamente usadas, assim como realizamos exemplos práticos usando dados reais com a intenção de familiarizar o leitor a situações cotidianas. Nossa recomendação é para sempre ter muito cuidado ao utilizar o risco relativo e a odds ratio, pois, ainda que possam não fazer sentido, são medidas facilmente calculadas em qualquer tipo de estudo. Bem, espero que tenhamos ajudado e até a próxima!
Ficou com dúvidas ou tem sugestões? Escreva para a gente: observatorioobstetricobr@gmail ou no nosso Twitter ou Instagram. Ah, e se gostou, compartilha lá em suas redes!
AGRESTI, Alan. Categorical data analysis. John Wiley & Sons, 2003.
DE BARROS LIMA, Andréa Maria Eleutério et al. DELINEAMENTOS DE ESTUDOS EPIDEMIOLÓGICOS E NÃO EPIDEMIOLÓGICOS DA ÁREA DA SAÚDE: UMA REVISÃO DE LITERATURA. Revista Unimontes Científica, v. 15, n. 2, p. 64-80, 2013.
WAGNER, Mário B.; CALLEGARI-JACQUES, Sidia M. Medidas de associação em estudos epidemiológicos. 1998.