
Linguagem R

14/12/2023
Linguagem R
Já parou para pensar em como analisar se diferentes médicos avaliando uma mesma ultrassonografia chegam ao mesmo diagnóstico? Ou como analisar se o peso indicado por diferentes balanças diverge? Ou se diferentes professores avaliam a redação de um aluno da mesma forma? O que todas esses casos têm em comum é que estamos interessados em saber se os resultados desses diferentes observadores ou instrumentos são consistentes, ou seja, se há uma concordância entre eles. Para obter essa resposta realizamos a chamada análise de concordância, que pode ser feita usando diferentes testes estatísticos, como o teste Kappa de Cohen e o coeficiente de correlação intraclasse, que serão abordados adiante.
Como mencionado, existem diversos testes que podem ser utilizados para avaliar a concordância, mas como saber qual o teste mais adequado para cada caso? Antes de responder essa pergunta, vamos relembrar alguns conceitos de variáveis.
Chamamos de variável uma característica a ser estudada que está presente em todos os elementos de uma população, podendo ser classificada como uma variável quantitativa ou uma variável qualitativa. Uma variável será considerada qualitativa quando for possível dividir os elementos da população em categorias com base em um atributo/ qualidade. Se essas categorias apresentarem uma ordenação ou hierarquia, a variável qualitativa é classificada como ordinal, caso contrário será nominal. Já a variável quantitativa é aquela que apresenta números como resposta, como medições e quantidades. Essas são consideradas discretas quando é possível listar todos os valores possíveis que essa variável pode assumir. Quando a variável pode assumir uma infinidade de valores em um intervalo específico, dizemos que a variável aleatória quantitativa é contínua.
Assim, vamos escolher o teste mais apropriado para avaliar a concordância com base na natureza da variável.
O teste Kappa de Cohen é baseado na porcentagem de concordância entre dois observadores, levando em consideração a porcentagem de concordância aleatória esperada. Assim, esse o coeficiente Kappa de Cohen é calculado usando:
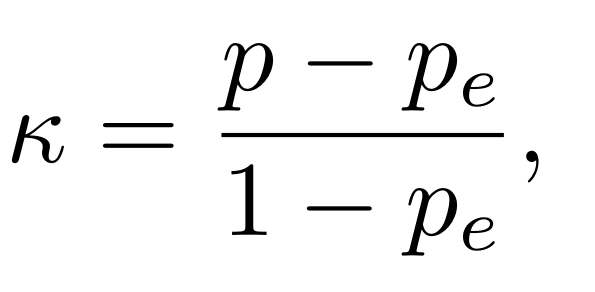
em que p representa a porcentagem de concordância entre os observadores e pe a porcentagem de concordância esperada aleatoriamente. Dessa forma, podemos interpretar esse coeficiente como a proporção de concordância entre observadores ajustada para a proporção de concordância esperada. Dessa forma, κ pode assumir valores no intervalo de 1 a -1, sendo que 1 indica concordância perfeita, 0 que a concordância não foi além do esperado e valores negativos mostram que a concordância foi pior que a esperada ao acaso.
Por exemplo, o diagnóstico de câncer de mama é feito por meio da avaliação de exames de imagem, como mamografias, por especialistas. Supondo que estamos coletando as informações de diagnóstico de dois radiologistas, podemos analisar a concordância entre eles usando a estatística κ. Abaixo estão as informações dos 100 casos analisados pelos dois profissionais:
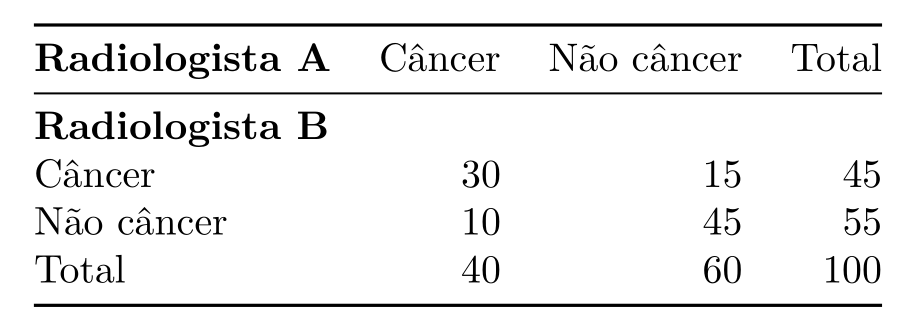
Analisando a tabela acima, podemos calcular κ da seguinte forma: como sabemos que p é a porcentagem de concordância, p será a soma do número de pacientes que foram diagnosticadas com câncer pelos dois radiologistas ou não câncer por ambos, dividida pelo total. Assim, p =(30+45)/100 = 0.75. Porém, sabemos que em parte desses casos a concordância pode ter ocorrido ao acaso, então precisamos também calcular p e para fazer essa correção. Visto que sabemos que 40/100 = 0.4 das pacientes foram diagnosticadas com câncer pelo radiologista A, 0.45 pelo radiologista B, 0.6 como não câncer pelo radiologista A e 0.55 pelo B, pe = (0.4)(0.45) + (0.6)(0.55) = 0.51. Com essas informações podemos encontrar o valor da estatística Kappa:
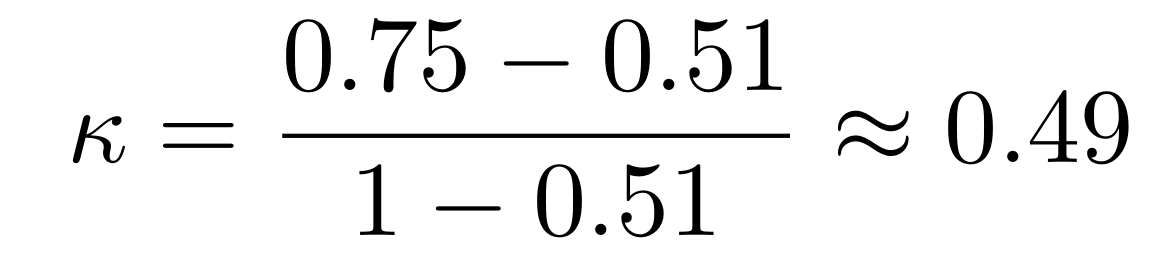
que indica uma concordância moderada entre os observadores.
Podemos realizar também esse teste utilizando o R, abaixo registramos os dados já apresentados na tabela e formando um dataframe, cujo começo é mostrado abaixo.


Em seguida, estamos carregando o pacote irr, que contém a função kappa2, utilizada para realizar o teste Kappa.


Essa função retorna o número de casos analisados em Subjects, já que 100 pacientes foram considerados; o número de examinadores em Raters, o valor da estatística Kappa em Kappa e o p-valor em p-value. Assim como calculamos, a função retorna o valor de κ = 0.49, indicando concordância moderada.
Vamos considerar agora que, além dos diagnósticos “Câncer” e “Não câncer”, os pacientes também possam ser classificados como “Suspeita menor” e “Suspeita maior”. Aqui podemos pensar que os observadores podem discordar em níveis diferentes, por exemplo, um paciente ser avaliado como “Câncer” e “Não câncer” pelos radiologistas A e B, respectivamente, é mais discrepante do que ser avaliado como “Câncer” e “Suspeita maior”. Por esse motivo, no teste de Kappa ponderado vamos atribuir “pesos” às diferentes concordâncias. Abaixo está a tabela com os diagnósticos das 100 pacientes avaliadas por esses especialistas.

Para calcular κ, precisamos primeiro pensar nas frequências esperadas, que são mostradas na tabela abaixo. Por exemplo, analisando a soma das linhas e colunas sabemos que a probabilidade do radiologista A diagnosticar uma paciente com câncer é de 21/100 = 0.21, enquanto para o radiologista B é de 20/100 = 0.20. Assim, calculamos que a probabilidade do diagnóstico de ambos ser câncer é (0.21)·(0.2) = 0.042 e a frequência esperada será 0.042 · 100 = 4.2. Usando o mesmo raciocínio, preenchemos a tabela abaixo:

No teste ponderado, vamos usar a matriz de pesos a seguir, em que quanto mais discrepantes são os diagnósticos, maior o peso arbitrário atribuído.

Agora, vamos calcular κw da seguinte forma:
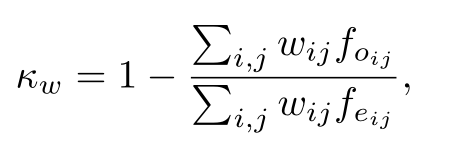
onde wij são os pesos atribuídos, foij são as frequências observadas e feij são as frequências esperadas.
Assim, no exemplo acima teremos:
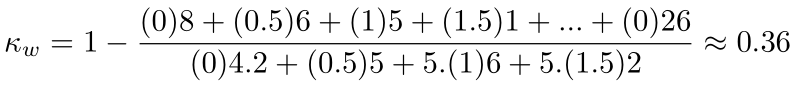
Esse teste também pode ser feito usando o pacote irr no R, veja abaixo:


Acima registramos os dados no R e criamos uma data frame identificando a paciente e quais foram os seus respectivos diagnósticos pelos dois radiologistas, denotando “câncer” como 1, “suspeita maior” como 2, “suspeita menor” como 3 e “não câncer” como 4. Agora vamos novamente usar a função kappa2 para realizar o teste, mas dessa vez vamos utilizar o argumento weight, que indica se o teste será ponderado e qual o tipo de ponderação, podendo ser unweighted (sem pesos), equal (ponderação linear) ou squared (ponderação
quadrática).


Ao contrário dos testes anteriores, em que o foco está no resultado observado por cada avaliador, o coeficiente de correlação intraclasse não se concentra apenas na concordância absoluta, mas também se as classificações relativas são semelhantes. É calculada da seguinte forma:

Assim, compara a variabilidade das diferentes classificações para um mesmo indivíduo com a variabilidade total. Esse valor pode variar de 0 a 1, sendo a maior proximidade a 1 indica que há uma similaridade entre as classificações de um mesmo observador e de 0 indica que as classificações de um mesmo grupo não são similares.
Como exemplo vamos usar a base de dados anxiety do R, em que três examinadores avaliam os níveis de ansiedade de vinte pacientes, classificando em uma escala de 1 a 6, em que quanto maior a pontuação atribuída, maiores os níveis de ansiedade.


Agora vamos usar a função icc() para calcular o coeficiente de correlação intraclasse.


Essa função tem como saída o modelo usado para calcular o coeficiente de concordância intraclasse (ICC), representado por Model, o tipo de ICC calculado em Type, número de casos observados em Subjects, o valor do coeficiente calculado em ICC, o valor da estaística F e o intervalo de confiança para o ICC. Assim, como o valor do coeficiente foi de 0.198, dizemos que houve baixa concordância.
Nesse post abordamos alguns testes e estatísticas usadas para medir a concordância entre observações de diferentes observadores, mas é importante lembrar que existem muitos outros testes para variáveis de diferentes natureza. Esperamos que as informações aqui mostradas tenham ficado claras e de fácil entendimento. Para comentários, dúvidas ou sugestões entre em contato em observatorioobstetricobr@gmail.com.
SPRENT, Peter.; SMEETON, Nigel C. Applied nonparametric statistical methods. 3rd e 4rd ed. Boca
Raton, Fla.: Chapman & Hall/CRC, 2001.
SIEGEL, Sidney. Estatística não-paramétrica: para as ciências do comportamento. São Paulo: McGraw-Hill,
1975, 1977, 1981.