
Linguagem R

15/03/2023
Linguagem R
De maneira geral, existem duas grandes áreas na inferência Estatística: a estimação de parâmetros (para mais informações sobre estimação, verifique nosso post sobre função de Verossimilhança), e o teste de hipóteses. Em particular, o teste de hipoteses consiste em avaliar uma afirmação a respeito de um parâmetro (média, variância, proporção, etc.) ou um conjunto de parâmetros. Tal afirmação recebe o nome de Hipótese Nula (denotado por H0), a afirmação alternativa recebe o nome de Hipótese Alternativa (denotado por H1).
Para deixar essa ideia um pouco mais clara, suponha que queremos saber se o tempo médio de internação por COVID (denotado por θ) é igual ou superior a 5 dias. Conseguimos reescrever essa indagação na forma de um sistema de hipóteses, a saber:
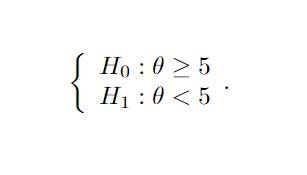
Para realizar o teste, assumimos que é possível obter uma amostra aleatória de tempo de internação de pessoas, X1,…,Xn, de uma distribuição f( . ; θ ). Tambem é necessário definir a estatística de teste (T) e região de rejeição (R). Estatística de teste é um valor calculado a partir da amostra, seu valor define a regra de rejeição para uma hipótese, ele mostra o quanto seus dados observados correspondem à distribuição esperada sob a hipótese nula desse teste estatístico, denotamos por R os possíveis valores para θ em que, dado a regra de rejeição, rejeitamos H0. Estamos interessados em saber se o tempo de internação é igual ou maior que 5 anos, ou em outras palavras H0 : θ ≥ 5. Um possível teste seria rejeitar H0 se ![]() <5−10/√n, onde
<5−10/√n, onde ![]() é a estatística de teste T, nesse caso nossa estatística acaba por ser o estimador de θ, digamos média amostral. No exemplo em questão, nossa região de rejeição são todos os possíveis valores de
é a estatística de teste T, nesse caso nossa estatística acaba por ser o estimador de θ, digamos média amostral. No exemplo em questão, nossa região de rejeição são todos os possíveis valores de ![]() <5−10/√n. Assumiremos δ como representação do procedimento de testes de hipótese no dercorrer do post.
<5−10/√n. Assumiremos δ como representação do procedimento de testes de hipótese no dercorrer do post.
Um teste pode ser tanto aleatório quanto não aleatório. O exemplo anterior, por exemplo, é um ótimo exemplo de teste não aleatório. Já um teste aleatório poderia ser “jogue uma moeda para o alto, caso cara rejeite a hipótese nula”. Tão importante quanto conhecer os tipos de teste é a verificação da “qualidade” de um teste, ou o quão correto estamos ao rejeitar uma hipótese. Podemos analisar esses resultados observando a função poder bem como os tipos de erros que podemos cometer dentro de um procedimento de testes de hipóteses.
Para cada teste aplicado sobre uma amostra obtida de uma distribuição f( . ; θ ) onde θ ∈ Θ em que Θ representa o espaço paramétricos de possíveis valores para θ, teremos uma função poder associada. A função poder define a probabilidade, dado um valor de θ, de rejeitar H0 dado que a mesma é falsa, ou seja, o quão acertivo foi nossa escolha dado o espaço paramétrico. Suponha um procedimento de teste δ, ou seja, possuímos uma regra de rejeição e uma estatística de teste obtidos através de uma amostra aleatória. A função π( θ | δ ) é chamada função poder do teste δ. Se S1 denota a região de rejeição de δ, então a função poder é determinada pela relação:
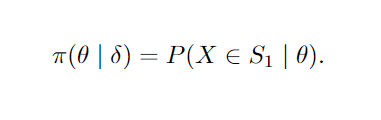
Se δ é descrito em função da estatística de teste T e da região de rejeição R, então:
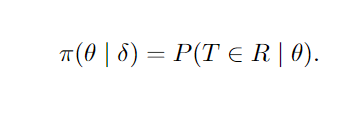
Para todo θ ∈ Θ.
Sendo a função poder, a probabilidade de rejeitar a hipótese nula dado os possíveis valores do parâmetro em estudo θ, buscamos o teste δ que minimize π(.) para os valores de θ pertencentes ao espaço paramétrico de H0 e a maximize quando θ pertence ao espaço paramétrico de H1, ou em outras palavras, π( θ ∈ Θ0 | δ )=0 e π( θ ∈ Θ1 | δ )=1, onde Θ0 representa o espaço paramétrico sob a hipótese nula e Θ1 o espaço paramétrico sob a hipótese alternativa.
Retomando o exemplo inicial onde rejeitamos a hipótese nula para ![]() < 5−10/√n, suponha que uma amostra aleatória de tempo de internação, X1,…,X20 foi obtida de uma distribuição Normal (θ,σ2), com σ2 conhecido e igual a 2, onde
< 5−10/√n, suponha que uma amostra aleatória de tempo de internação, X1,…,X20 foi obtida de uma distribuição Normal (θ,σ2), com σ2 conhecido e igual a 2, onde ![]() é o estimador de máxima verossimilhaça para média amostral. Obtendo, assim, a seguinte função poder
é o estimador de máxima verossimilhaça para média amostral. Obtendo, assim, a seguinte função poder
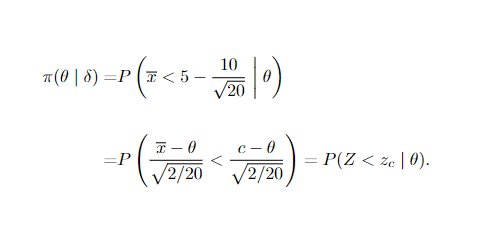
Onde Z segue uma distribuição Normal(0,1), e c = 5 – 10/√20 obtendo assim:
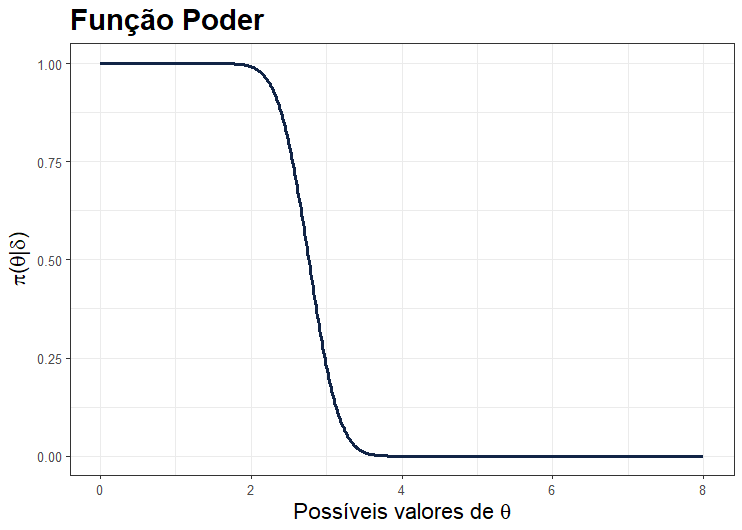
Perceba que, para os valores de θ dentro do espaço paramétrico de H0 (θ ≥ 5) o valor para função poder é 0. Para replica da função poder como apresentada acima no software de programção R basta gerar possíveis valores de θ, digamos entre 0 e 8, e para cada um desses valores calcular o quantil z crítico obtido a partir da constante c e dos valores gerados do parâmetro. Como segue:
#Gere valores de theta
theta <- seq(0,8,by = 0.01)
#Calcule c e a partir dele e de theta calcule os z criticos
c <- 5 - (10/sqrt(20))
zc <- (c - theta)/(sqrt(2/20))
#Calcule a funcao poder
pi.theta <- pnorm(zc,0,1,lower.tail = T)
#Esboce o grafico
library(ggplot2)
df <- cbind(theta,pi.theta) %>% as.data.frame()
df %>%
ggplot() +
aes(x = theta, y = pi.theta) +
geom_line(size = 1.1, colour = “#112446”) +
labs(
x = expression(paste(“Possíveis valores de “,
theta)),
y = expression(paste(pi,
“(“,
theta,
“|”,
delta,
“)”)),
title = “Função Poder”
) +
theme_bw() +
theme(
plot.title = element_text(size = 20L,
face = “bold”),
axis.title.y = element_text(size = 15L,
face = “bold”),
axis.title.x = element_text(size = 15L,
face = “bold”)
)
Ao considerar como possível escolha, rejeição ou não rejeição da hipótese nula, testamos uma hipótese contra a outra. Dentro deste cenário encontramos dois tipos de erros, os chamados:
É possível indicar a probabilidade de ocorrência de cada erro, para o exemplo trabalhado na sessão, por meio da seguinte notação para o Erro do Tipo I:
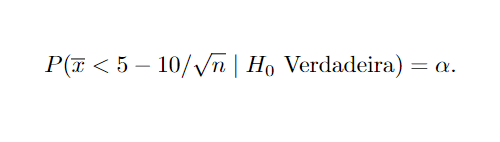
Para o Erro do Tipo II:
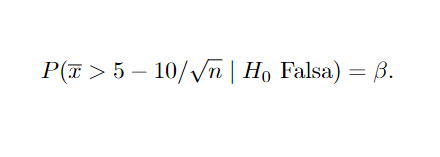
As hipóteses de um teste podem ser da forma simples ou composta. Uma hipótese simples, é aquela onde o espaço de possíveis valores de θ é definido em apenas um ponto, dessa forma a distribuição do parâmetro é completamente especificada ( H0 : θ = θ0 , f(. ; θ0 ) , ou ainda H0: θ = 5 ). Por outro lado, uma hipótese composta é aquela cuja distribuição não é especificada completamente e θ pode assumir um conjunto de valores Θ ( H0 : θ ∈ Θ, f( . ; Θ ), ou H0 : θ ≥ 5). Uma forma de introduzir o tema, é observar primeiro o contexto de Hipóteses simples versus Hipótese simples, ou em outras palavras:
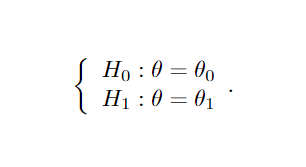
Suponha que temos uma amostra aleatória X1, …, Xn de uma distribuição com parâmetro θ que pode ser θ0 ou θ1. Para testar a hipótese nula H0: θ = θ0 versus a hipótese alternativa H1 : θ = θ1, podemos utilizar um teste de razão de verossimilhança. Esse teste envolve a comparação da função de verossimilhança L(x1,…,xn) associada à densidade f( ⋅ ), utilizando a razão λ = L0( ⋅ ) / L1( ⋅ ), onde L0( ⋅ ) e L1( ⋅ ) representam as funções de verossimilhança quando θ = θ0 e θ = θ1, respectivamente. Se λ é menor do que uma constante não negativa k, rejeitamos a hipótese nula, sugerindo que a amostra pode vir de uma população com distribuição f1( ⋅ ) em vez de f0(⋅). Por exemplo, podemos testar o tempo médio de internação, agora digamos H0 : θ = 5 versus H1 : θ = 7 (onde θ ainda representa o tempo de internação médio em dias), para uma amostra aleatória de uma distribuição normal N(θ,1), utilizando a função de verossimilhança.
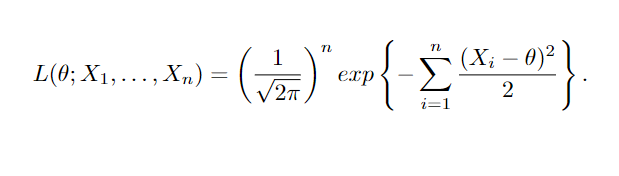
Obtendo o teste de razão de verossimilhança,
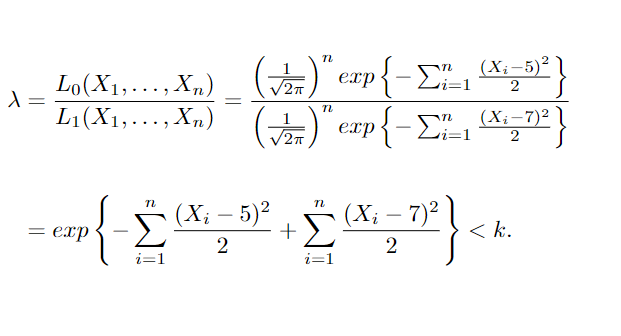
Que pode ser reescrito como:
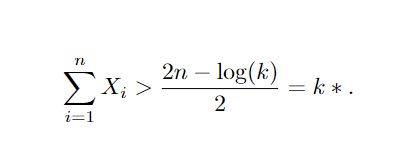
Ou seja, rejeitamos H0 para um somatório de Xi maior que alguma constante k*. Suponha uma amostra de ∑Xi = 36, rejeitamos H0 se 36>(12−log(k))/2 note que, para a amostra em questão, temos um valor de λ extremamente baixo, logo podemos rejeitar a hipótese de tempo de duração igual a 5 dias, optando pela alternativa de 7 dias de duração, ou em outras palavras, os dados obtidos pela amostra mostram indícios de que a distribuição original da população não siga a proposta pela hipótese nula, e sim pela alternativa.
Para cada k fixado temos um teste diferente. Uma forma de verificar o melhor k descrito é pela análise da função poder, discutida anteriormente, para cada um dos testes, que pode ser visto também pela análise do teste Mais Poderoso, que minimize o erro proveniente do processo de teste de hipótese.
Antes de falar sobre os testes mais poderosos, uma definição deve ser esclarecida: o tamanho do teste. Vamos admitir um teste δ cuja hipótese nula seja H0: θ ∈ Θ0 ( H0 : θ < θ0, ou H0 : θ = θ0 por exemplo), em que Θ0 ⊂ Θ(ou seja, Θ0 é um subconjunto do espaço paramétrico Θ). Assim, o tamanho do teste é definido como sup[π( θ ∣ δ ) ∣ θ ∈ Θ0] onde π( θ ∣ δ ) é a função poder de θ dado o procedimento de teste δ. Ou em outras palavras, o valor para θ dentro do espaço paramétrico da hipótese nula que maximiza a função poder associada ao procedimento de teste de hipótese δ.
Esclarecida essa definição, daremos prosseguimento ao assunto. Assim como já comentado, queremos um teste δ em que π( θ0 ∣ δ ) = P(Rejeitar H0 | H0 verdadeiro) seja a menor possível e que π( θ1 ∣ δ ) = P(Rejeitar H0 | H0 falsa) seja a maior possível. Em um mundo ideal, π( θ1 ) = 1 e π( θ0 ) = 0, isto é, quando os erros do tipo I e II são minimizados simultâneamente. Entretanto, na prática, uma das metodologias aplicadas, como já citado, de forma a definir o melhor teste possível é minimizar o erro do tipo II fixando o erro do tipo I.
Teste Mais Poderoso: Um teste δ∗ em que H0 : θ = θ0 contra H1 : θ = θ1 é definido como teste mais poderoso de tamanho α, com 0 < α < 1, se e somente se:
Ou seja, podemos considerar um teste δ∗ como sendo o teste mais poderoso se, para qualquer outro teste de tamanho menor ou igual a α, ele possuir o maior poder.
O lemma a seguir é muito útil para encontrar testes mais poderosos.
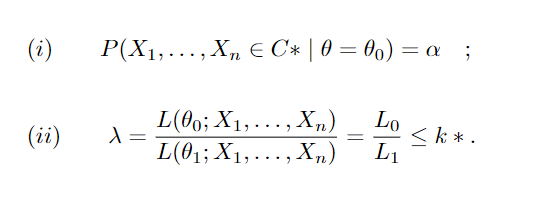
E λ > k* se (x1, ..., xn) ∈ C* . Onde C é a região de rejeição e C* seu complementar.
Então, considerando um teste de hipóteses simples, temos que o teste para essa região de rejeição é o teste mais poderoso. Vamos mostrar um exemplo para melhor compreensão. Seja X1, …, Xn uma amostra aleatória de tipos de parto, onde estamos interessados em saber a proporção de partos por cesária para um determinado município, para isso suponha que a amostra segue distribuição Bernoulli( θ), onde Xi=1, foi cesária e Xi=0 caso contrário. Seja o teste H0 : θ = θ0 vs. H1 : θ = θ1, θ1 > θ0 onde θ representa a proporção de partos por cesária. Então
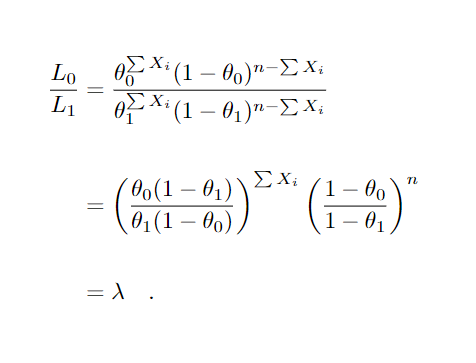
Rejeitamos H0 para um λ ≤ k∗, note porém, que λ
varia em função da amostra X1, …, Xn. Podendo considerar as outras informações como constantes, nos levando a rejeitar H0 se ∑Xi≥k′. Para compreender suponha θ1 = 0.5 e θ0 = θ = 0.3 e uma amostra de tamanho 10.
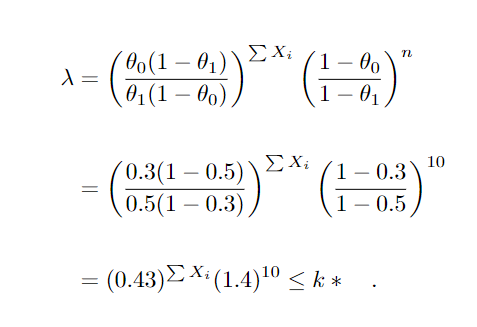
Conforme incrementamos o valor do somatório, diminuimos o valor de λ, logo rejeitamos H0 para um valor do somatório maior que uma constante k′, ou seja, rejeitamos a hipótese de que a proporção de partos por cesária seja 0.3 e optamos pela proporção de 0.5 caso o número de cesarianas seja relativamente alto.
Perceba porém, que ao trabalharmos com uma variável de contagem ( ∑Xi∼Binomial(n,θ)), não se torna tão simples assim fixar o valor de α de forma arbitrária como fariamos em um teste para variáveis contínuas para encontrar o teste mais poderoso, já que k∗ pode assumir apenas valores inteiros. Lembrando que α = P( ∑Xi ≥ k′∣ θ = 0.3), fazendo o processo inverso, onde fixamos os possíveis valores de k′ ( 0 ≤ k′ ≤ 10), obtemos os seguintes tamanhos de teste α:

Ou seja, o teste mais poderoso de tamanho α=0.15 é aquele em que rejeitamos H0 para um ∑Xi≥4, e assim sucessivamente.
Note que o teste mais poderoso de tamanho α, dado o lemma de Neyman-Pearson é necessariamente um teste de razão de verossimilhança simples.
Generalizaremo, agora, para os teste de hipóteses compostas. O método mais geral para testar hipóteses, que, geralmente não é o que fornece resultados mais precisos, mas é aplicável em todo tipo de situação, é o Teste de Razão de Verossimilhança Generalizado. Considere X1, …, Xn uma amostra aleatória obtida de uma função de densidade f( x ; θ), θ ∈ Θ, e um teste do tipo H0: θ ∈ Θ0 contra H1: θ ∈ Θ1 = Θ −Θ0
Teste de Razão de Verossimilhança Generalizado: suponha L(θ; X1, …, Xn) a função de verossimilhança para a amostra X1, …, Xn. O teste de razão de verossimilhança generalizada, denotado por λ, é definido como:
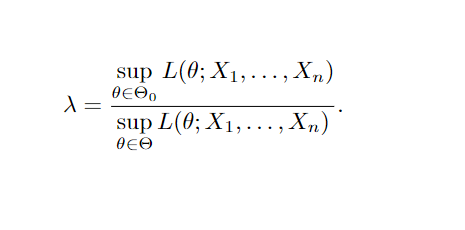
Onde λ se torna uma função da amostra definida no intervalo [0,1]. Assim como no Teste de Razão de Verossimilhança para hipóteses simples, rejeitamos a hipótese nula ( H0) se o valor de λ for menor ou igual a uma constante k∗ definida no intervalo [0,1]. Quanto mais próximo de 1 for o valor de λ, mais difícil será rejeitar a hipótese nula, pois indica que o valor que maximiza a função de verossimilhança dentro do espaço paramétrico da hipótese nula está se aproximando do valor que maximiza para o espaço paramétrico total.
Suponha o exemplo onde testamos H0 : θ ≥0.5 versus H1 : θ < 0.5, sendo θ a proporção de partos naturais, e que possuimos uma amostra X1, …, X30 ∼Bernoulli(θ), onde ∑Xi=12. Primeiro, faremos de forma geral onde 0.5 = θ0 e depois substituiremos pelos valores propostos. Então, o teste de razão de verossimilhança pode ser definido como:
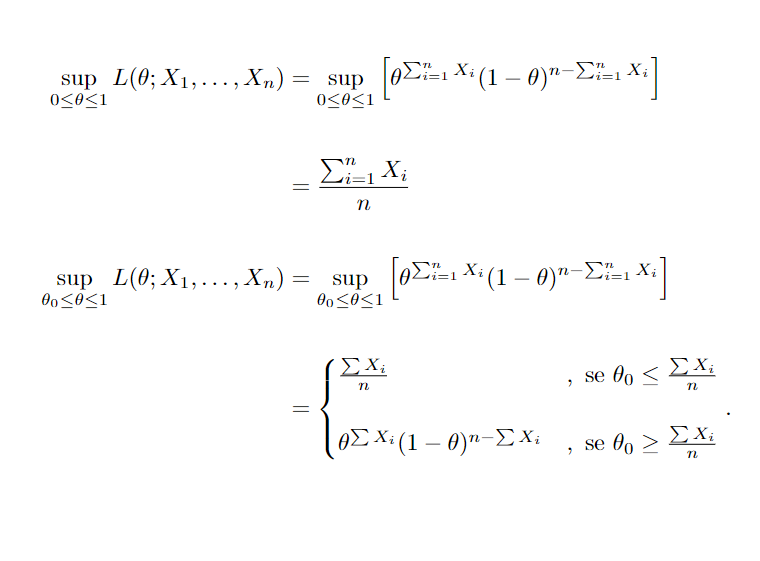
Assim,
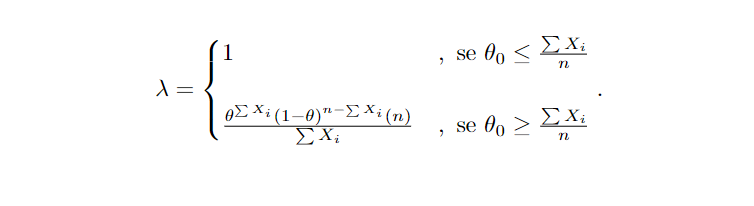
Substituindo pelos valores propostos no problema então obtemos que λ=0,00000000233, pois 0.5 ≥ ∑Xi /n, rejeitando H0 para um λ < k. É possível notar, porém, que λé função de ∑Xi e que λ é descrescente conforme incrementado o valor de ∑Xi, logo rejeitamos H0 para um ∑Xi > k′.
Testes Uniformemente Mais Poderosos (UMP): um teste δ∗ do tipo H0: θ ∈ Θ0 contra H1: θ ∈ Θ1 = Θ – Θ0 é definido como UMP de tamanho α se e somente se
(i) sup[π( θ ∣ δ ) ∣ θ ∈ Θ0] = α;
(ii) π( θ ∣ δ* )> π( θ ∣ δ ) para todo θ ∈ Θ−Θ0 e para qualquer teste δ de tamanho menor ou igual a α.
Note que na verdade o teste UMP é a generalização do apresentado para teste de hipóteses simples agora no cenário em que possuímos um intervalo de possíveis valores para o paramêtro. Voltando ao exemplo acima, sabemos que rejeitamos H0 se ∑Xi>k′, então, supondo que queremos o teste UMP de tamanho α = 0.05, basta encontrar o quantil da distribuição Binomial(30,0.5), que acumule 0.05 de probabilidade na calda a esquerda. Por apoio computacional com o software R, basta atribuir a função qbinom() os valores para obter o quantil que acumule os 0.05 de probabilidade na calda a direita, como segue:
alpha = 0.05
n= 30
theta = 0.5
qbinom(p = alpha, size= n, prob = theta, lower.tail = F)
Obtendo o valor de 19, ou seja, o teste UMP de tamanho α = 0.05 é aquele em que rejeitamos H0 para um ∑Xi > 19.
Na literatura, podemos encontrar formas diferentes de testar hipóteses das vistas neste tutorial, mas elas fogem do escopo deste post e por ter como objetivo a introdução aos métodos mais utilizados, não foram abordadas aqui. Para uma outra metodologia mais simples onde são apresentados principalemente o t-test e teste normal para média populacional recomenda-se a leitura do livro de introdução a estatística (Magalhães and De Lima 2002). Para uma abordagem mais aprofundada do tema bem como os aqui apresentados e mais exemplos a respeito, é recomendada (Schervish and DeGroot 2012) bem como (Mood 1950). Espero que o texto tenha sido esclarecedor e de ajuda ao leitor. Para mais informações ou dúvidas, escreva-nos em : comunicacao@observatorioobstetricobr.org