Introdução

Os testes de homogeneidade proporcionam uma abordagem essencial para avaliar a consistência da associação entre duas variáveis digamos X e Y, desempenhando importante aplicação, particulamente em estudos relacionados à saúde materna. Entre esses testes, destaca-se o teste de Breslow-Day, uma ferramenta estatística inicialmente proposta por Breslow e Day em 1980 (Breslow e Day 1980). Ao contrário de outros métodos, o teste de homogeneidade de Breslow-Day não se limita a uma análise de tabelas 2×2, como vemos no teste qui-quadrado de homogeneidade, expandindo sua aplicabilidade para verificar a homogeneidade das razões de chances (odds ratios) em diferentes níveis de uma terceira variável, chamada de estratificadora. Aqui, entretanto, não estenderemos a explicações maiores sobre razões de chances. Para melhor informação a respeito do tema, recomendamos a leitura deste outro tutorial já publicado pelo OOBr.
Um exemplo ilustrativo da relevância do teste de Breslow-Day em contextos relacionados à saúde materna é evidenciado ao analisarmos se a relação entre a administração de um tratamento e a incidência de complicações durante a gravidez permanece consistente de acordo com o estado nutricional da gestante, que poderia ser denotado por exemplo, a e b. Aqui, o estado nutricional da gestante seria a variável estratificadora, e a e b seriam seus estratos. Assim, nosso objetivo seria testar se o tratamento aplicado tem a mesma influência em complicações na gravidez para ambos os estados nutricionais a e b.

Este texto pressupõe que o leitor possui conhecimentos prévios em conceitos básicos relacionados à teoria de testes de hipóteses. Caso contrário, ou para uma revisão desses conceitos, recomendamos a leitura do post sobre testes de hipóteses produzido pelo OOBr, disponível neste link.

O teste de Breslow-Day

O teste de Breslow-Day é uma ferramenta estatística robusta projetada para avaliar a homogeneidade das razões de chances (odds ratios) em diferentes estratos de uma variável estratificadora. Sua aplicação se destaca em estudos epidemiológicos, particulamente na área da saúde materna, onde a complexidade das interações entre variáveis exige métodos analíticos refinados. É um teste não paramétrico, logo, não assumimos nenhuma suposição a respeito da distribuição dos dados da amostra.

O primeiro passo, como na aplicação de qualquer teste estatístico, é a definição das hipóteses em análise. As hipóteses para o teste de Breslow-Day, levando em consideração o exemplo de complicação na gravidez nos dois estratos de estado nutricional, são:

• H₀: Não há diferença na razão de chances entre o tratamento aplicado e complicações nos diferentes estratos definidos pela variável estratificadora (por exemplo, estado nutricional da gestante).
• H₁: Existe diferença na razão de chances entre o tratamento aplicado e complicações nos diferentes estratos definidos pela variável estratificadora.

A fórmula para o cálculo do teste de Breslow-Day envolve os elementos de uma tabela de contingência, podemos ver na Tabela 1 um exemplo deste tipo de tabela para o k-ésimo estrato. No nosso caso, k = 1,2.

Em que:

• a_k é o número de indivíduos que passaram pelo tratamento e tiveram complicações no k-ésimo estrato da variável estratificadora;
• b_k é o número de indivíduos que passaram pelo tratamento e não tiveram complicações no k-ésimo estrato da variável estratificadora;
• c_k é o número de indivíduos que não passaram pelo tratamento e tiveram complicações no k-ésimo estrato da variável estratificadora;
• d_k é o número de indivíduos que não passaram pelo tratamento e não tiveram complicações no k-ésimo estrato da variável estratificadora;
• m_Ck é o número de indivíduos totais que tiveram complicações no k-ésimo estrato da variável estratificadora;
• m_Sk é o número total de indivíduos que não tiveram complicações no k-ésimo estrato da variável estratificadora;
• n_Tk é o número total de indivíduos que passaram pelo tratamento no k-ésimo estrato da variável estratificadora;
• n_Sk é o número total de indivíduos que não passaram pelo tratamento no k-ésimo estrato da variável estratificadora;
• T_k é o número total de indivíduos no k-ésimo estrato da variável estratificadora.

A partir destas informações, geramos a estatística de teste Χ²_BD, onde Χ²_BD é distribuído assintoticamente como uma qui-quadrado com K-1 graus de liberdade, sendo K o número total de estratos da variável estratificadora. A estatística de teste é calculada pela seguinte fórmula:

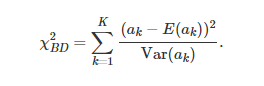
A soma em acima não inclui os casos (estratos) envolvendo tabelas com frequências marginais nulas, uma vez que nestes casos a variância Var(a_k) seria zero.

O valor esperado e a variância da frequência $a_k$ são obtidos sob a premissa de homogeneidade da razão de chances. O valor esperado E(a_k) é obtido como uma solução da equação quadrática

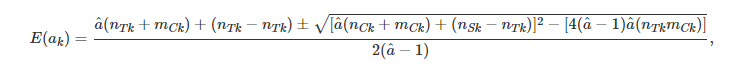
em que â é o estimador de Mantel-Haeszel da razão de chances comum (Mantel e Haenszel, 1959):

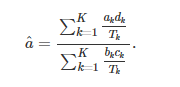
Adicionalmente, a variância Var(a_k) é expressa como:

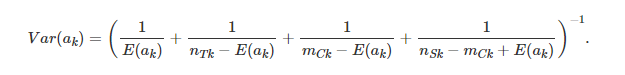
Assumindo a hipótese nula como verdadeira, conforme discutido no post sobre teste de hipótese ou valor-p, recorremos à distribuição qui-quadrado para avaliar a probabilidade de obter um valor tão extremo quanto o observado. Esse procedimento fornece evidências para a rejeição ou não rejeição da hipótese nula. Assumido um valor de significância, caso o valor observado seja significativamente extremo, em termos estatísticos, rejeitamos a hipótese nula, indicando evidências de heterogeneidade nas razões de chances entre os estratos. Caso contrário, não temos evidências suficientes para rejeitar a hipótese nula, sugerindo consistência nas associações. Seguiremos com um exemplo prático com a utilização do software estatístico R para melhor entendimento do teste. Os dados são meramente ilustrativos, simulados no próprio R de maneira simples.

Aplicação

Vamos ilustrar a aplicação do teste de Breslow-Day em dois exemplos práticos relacionados à obstetrícia.

Exemplo 1: Influência do Tipo de Parto na Incidência de Complicações Neonatais

Neste cenário, consideraremos um estudo que investiga se o tipo de parto (normal ou cesariana) influencia a incidência de complicações neonatais, estratificando por duas idades gestacionais: prematuro e a termo. Gerando duas tabelas,uma para cada um dos K = 2 estratos trabalhados, onde investigamos a homogeneidade da razão de chances entre as variáveis de Tipo de Parto e complicação no parto.

Usando o R, podemos construir tabelas de contigência de maneira simples, utilizando a função xtabs do pacote base, como especificado no código. Onde vemos a variável estratificadora entrando como terceira variável da soma (Idade_gestacional).

# Criação da tabela de contingência
tabela_contingencia_obstetricia1 <- xtabs(Frequencia ~ Tipo_Parto + Complicacoes + Idade_Gestacional, data = dados_obstetricia1) tabela_contingencia_obstetricia1

## , , Idade_Gestacional = A Termo
##
## Complicacoes
## Tipo_Parto Nao Sim
## Cesariana 94 68
## Normal 6 4
##
## , , Idade_Gestacional = Prematuro
##
## Complicacoes
## Tipo_Parto Nao Sim
## Cesariana 17 12
## Normal 25 30

Aplicamos o teste pela função BreslowDayTest() do pacote DescTools, onde podemos obter o valor da estatística de teste, os graus de liberdade e o respectivo p-valor do teste. A função permite a especificação de uma razão de chances comum referente a hipótese nula. Caso esse argumento não seja especificado, a função estima essa razão de chances comum utilizando o já apresentado estimador de Mantel-Haenszal.

# Aplicação do teste de Breslow-Day
#install.packages(‘DescTools’)
library(DescTools)
resultado_teste_obstetricia1 <- BreslowDayTest(tabela_contingencia_obstetricia1) pvalue <- resultado_teste_obstetricia1$p.value resultado_teste_obstetricia1

##
## Breslow-Day test on Homogeneity of Odds Ratios
##
## data: tabela_contingencia_obstetricia1
## X-squared = 0.57493, df = 1, p-value = 0.4483

Com um valor-p igual a 0.4483055, não encontramos evidências estatisticamente significativas para rejeitar a hipótese nula. Portanto, não temos motivos para acreditar que o tipo de parto influencie de maneira diferente em complicações neonatais quando comparamos idades gestacionais prematuras ou a termo.

Exemplo 2: Influência do Tipo de Anestesia na Incidência de Complicações Pós-Parto nos diferentes extratos do baixo peso ao nascer

Neste cenário, consideraremos um estudo que investiga se o tipo de anestesia (Epidural ou Sem Anestesia) influencia a incidência de complicações neonatais, estratificando por três intervalos de peso baixo ao nascer: menos que 1500g (< 1500), entre 1500g e 1999g (1501 < peso < 2000) e 2000g a 2499g (1999 < peso < 2500). Evoluímos então para um cenário onde temos K=3 estratos, além de que uma das tabelas possúi um valor marginal nulo, veremos como isso afeta nosso teste.

, , peso = < 1500 Complicacoes_Pos_Parto Tipo_Anestesia Nao Sim Epidural 24 0 Sem Anestesia 18 74 , , peso = 1501 < peso < 2000 Complicacoes_Pos_Parto Tipo_Anestesia Nao Sim Epidural 75 78 Sem Anestesia 53 5 , , peso = 1999 < peso < 2500 Complicacoes_Pos_Parto Tipo_Anestesia Nao Sim Epidural 88 11 Sem Anestesia 49 93

# Teste de Breslow-Day
resultado_teste_obstetricia4 <- BreslowDayTest(tabela_contingencia_obstetricia4) resultado_teste_obstetricia4

##
## Breslow-Day test on Homogeneity of Odds Ratios
##
## data: tabela_contingencia_obstetricia4
## X-squared = 127.38, df = 2, p-value < 2.2e-16

O valor-p extremamente baixo (< 0.001) indica que há evidências estatisticamente significantes de heterogeneidade nas odds ratios entre os diferentes estratos de peso ao nascer. Em outras palavras, a associação entre o tipo de anestesia e a incidência de complicações pós-parto não é homogênea nos grupos de peso ao nascer considerados. Portanto, com base nos resultados deste teste, podemos concluir que a influência do tipo de anestesia na incidência de complicações pós-parto varia significativamente entre os grupos de peso ao nascer delineados. Mas e caso a tabela citada não possúisse valor nulo? vamos verificar abaixo.

## , , peso = < 1500 ## ## Complicacoes_Pos_Parto ## Tipo_Anestesia Nao Sim ## Epidural 24 6 ## Sem Anestesia 18 74 ## ## , , peso = 1501 < peso < 2000 ## ## Complicacoes_Pos_Parto ## Tipo_Anestesia Nao Sim ## Epidural 75 78 ## Sem Anestesia 53 5 ## ## , , peso = 1999 < peso < 2500 ## ## Complicacoes_Pos_Parto ## Tipo_Anestesia Nao Sim ## Epidural 88 11 ## Sem Anestesia 49 93

# Teste de Breslow-Day
resultado_teste_obstetricia5 <- BreslowDayTest(tabela_contingencia_obstetricia5) resultado_teste_obstetricia5

##
## Breslow-Day test on Homogeneity of Odds Ratios
##
## data: tabela_contingencia_obstetricia5
## X-squared = 114.45, df = 2, p-value < 2.2e-16

Vemos uma redução na estatística de teste, mas ainda sim, com valor-p extremamente baixo (< 0.001), confirmando a hipótese anteriormente citada.

Considerações Finais

O teste de Breslow-Day é uma ferramenta estatística poderosa para avaliar a homogeneidade das razões de chances em diferentes estratos de uma variável estratificadora. Ao aplicar esse teste, consideramos a hipótese nula de que não há diferença na associação entre as variáveis de interesse nos estratos definidos. Em contrapartida, a hipótese alternativa sugere a presença de diferenças significativas nas associações entre os estratos.

Ao analisar a estatística de teste Χ²_BD, com seus graus de liberdade e p-valor associados, podemos tomar decisões informadas sobre a rejeição ou não rejeição da hipótese nula. Um p-valor inferior ao nível de significância escolhido (geralmente 0.05) sugere evidências estatísticas para rejeitar a hipótese nula, indicando heterogeneidade nas razões de chances entre os estratos. Por outro lado, um p-valor maior sugere a falta de evidências para rejeitar a hipótese nula, indicando consistência nas associações.

É importante interpretar os resultados considerando o contexto específico do estudo e a relevância clínica das associações analisadas. O teste de Breslow-Day oferece uma abordagem estatística valiosa para investigações epidemiológicas mais complexas, especialmente na área da saúde materna, onde a heterogeneidade nas associações é comum devido à diversidade de fatores envolvidos.

Utilizar o teste de Breslow-Day com sabedoria, contribui para a qualidade e confiabilidade das análises estatísticas em estudos estratificados. Esperamos que este tutorial tenha sido útil para a compreensão e aplicação desse teste em seus próprios estudos e pesquisas. Se tiver dúvidas ou sugestões, sinta-se à vontade para entrar em contato pelos nossos canais de comunicação.

Referências

Breslow, Norman E., Nicholas E. Day, and Elisabeth Heseltine. “Statistical methods in cancer research.” (1980): 248-279.