Introdução

Muitos dos dados usados por estatísticos, pesquisadores e analistas variados são provenientes de amostras e não de todos os elementos de uma população. Diante desse contexto, muito se fala da necessidade em se considerar a distribuição amostral como mecanismo fundamental na execução de procedimentos inferenciais. Mas, o que de fato expressa a distribuição amostral? Por que ela é de suma importância para a análise inferencial? Nesse post vamos explorar o conceito de distribuição amostral, desvendar suas propriedades e exemplificar seu uso por meio da investigação da média amostral e da proporção amostral, mas antes vamos discutir um pouco sobre parâmetros e estatísticas para uma melhor compreensão do tema.

Parâmetros e estatísticas

Chamamos de parâmetro toda a medida usada para resumir alguma característica da variável de interesse na população. Por exemplo, suponha que tenhamos interesse em investigar o peso médio de recém-nascidos de uma população e o façamos através do uso de algumas medidas-resumo, tais como o peso médio ou mediano dos recém-nascidos ou a variância desses pesos na população. Como essas são medidas relacionadas à população, cada uma delas representa um parâmetro. Na prática, será que é fácil obter essas medidas no contexto de todos os recém-nascidos de uma população? Muitas vezes, quando temos o interesse em analisar algum parâmetro, não conseguimos analisar todos os seus elementos devido a diversos fatores, como a extensão da população, demora ou falta de recursos, exigência de testes destrutivos, entre outros. Nesses casos optamos pela coleta de amostras, que devem ser representativas da população.

Um método de amostragem útil para obter amostras representativas da população é a “amostragem aleatória simples”, que consiste no sorteio de n elementos da população para comporem a amostra, sendo que todos os elementos têm igual probabilidade de serem selecionados. Essa amostragem pode ser feita com reposição, ou seja, um mesmo elemento pode ser sorteado mais de uma vez, ou sem reposição, em que cada elemento pode ser selecionado apenas uma vez. Nesse post usaremos a amostragem aleatória simples com reposição, por trazer vantagens matemáticas e estatísticas, como, por exemplo, a independência entre as unidades sorteadas.

Voltando ao problema do peso médio de recém-nascidos, uma vez que temos dificuldades em analisar todos os bebês de uma população e obter um valor para o parâmetro, vamos recorrer ao uso de amostras e analisar nesses conjuntos a medida de interesse, aqui, o peso médio dos bebês. Vimos que na população essa característica resumo de interesse é denominada parâmetro, mas quando consideramos essa mesma característica no âmbito da amostra temos a chamada estatística ou, quando buscam aproximar o valor de um parâmetro, de estimador. Dessa forma, o peso médio de recém-nascidos em uma população corresponde ao parâmetro e o peso médio de recém-nascidos na amostra corresponde ao estimador/estatística.

O papel da distribuição amostral

Suponha que em uma população de 10000 bebês recém-nascidos, tenhamos selecionado 20 bebês via aas, com reposição. Para implementar esse problema no RStudio e gerar os pesos de 10000 bebês recém-nascidos, vamos supor que a variável peso se comporte segundo uma distribuição normal na população, com média de 3.1 kg e desvio-padrão de 0.49 kg. No código abaixo criamos os elementos da população, obtivemos que sua média foi 3.1 (parâmetro) e selecionamos uma primeira amostra de tamanho 20, a qual denominamos a1, por meio da função sample(). Na função sample o primeiro argumento representa a população da qual as amostras serão retiradas, em seguida o tamanho amostral, nesse caso 20, e quando definido como verdadeiro (“True”), o terceiro argumento representa que a amostragem será com reposição. Vale ressaltar que na grande maioria dos problemas práticos, os parâmetros são desconhecidos. O que faremos agora é estudar o comportamento dos estimadores e relacioná-los com os parâmetros.

Abaixo apresentamos os pesos dos 20 bebês (unidades amostrais) que compõe a amostra e uma estimativa do peso médio, que foi aproximadamente 3.242 kg. Estimativa nada mais é que o estimador calculado para uma amostra observada.

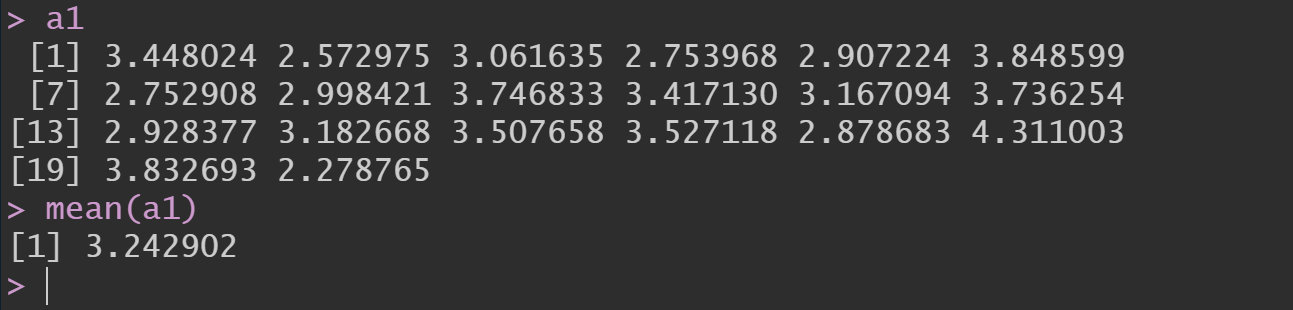
Será que se selecionássemos um outro conjunto de 20 bebês dessa população, usando o mesmo método de amostragem, obteríamos exatamente a mesma estimativa de peso médio, ou seja, 3.242 kg? Para responder a essa pergunta, vamos gerar uma segunda amostra de mesmo tamanho, chamada a2.

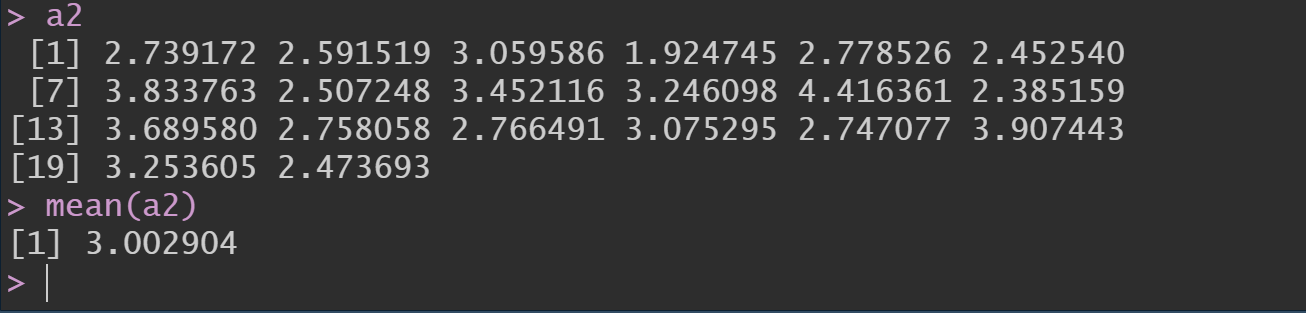
Esses foram os pesos obtidos em a2, cujo peso médio estimado foi 3.002 kg. Logo, amostras diferentes apresentaram médias amostrais diferentes, o que nos leva a concluir que o peso médio fornecido pela amostra dependerá dos valores dos pesos presentes nela, ou seja, o peso médio será uma função dos pesos observados em cada amostra. E é aqui que aparece o conceito de distribuição amostral. A distribuição amostral de um estimador é uma distribuição de probabilidades que nos ajuda a entender como as estatísticas amostrais variam de amostra para amostra, desde que essas amostras tenham sempre o mesmo tamanho e sejam retiradas de uma mesma população.

Generalizando essa conclusão, podemos interpretar que para cada amostra obteremos uma estimativa diferente, assim a distribuição amostral terá o papel de nos ajudar a entender a distribuição do estimador, que também é uma variável aleatória. Dessa forma, podemos definir a distribuição amostral como a distribuição de probabilidades de uma estatística T, usando amostras aleatórias simples de tamanho n. Essa estatística T será uma função da amostra (X1,…,Xn), sendo assim T=ƒ(X1,…,Xn).

Distribuição amostral da média

Agora que entendemos o conceito de distribuição amostral e a sua função, vamos explorá-la ainda no contexto de achar aproximações para o peso médio de recém nascidos na população. Porém, dessa vez, usaremos a distribuição dos pesos médios de 100 amostras (réplicas), todas de tamanho 30, dos pesos dos recém-nascidos, obtidos via amostragem aleatória simples, com reposição.

Primeiro vamos entender os comandos abaixo:

Aqui estamos chamando de n o tamanho de cada amostra e de a o número de réplicas. M representa uma matriz de zeros que acomodará em cada linha uma réplica da amostra de tamanho 30, em que a última coluna representa a média dessa linha, ou seja, a média dos pesos coletados em cada réplica. Obteremos uma matriz nesse formato:

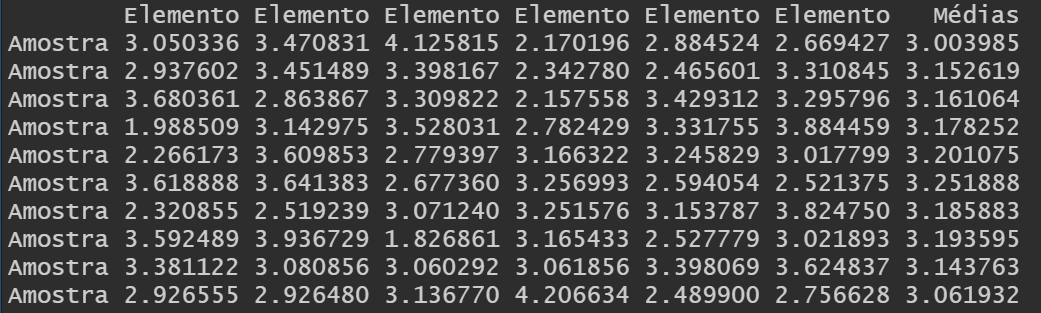
Tenha em mente que foi mostrado apenas um pedaço da matriz, já que ela apresenta 100 linhas e 31 colunas no total, dos quais as 30 primeiras colunas apresentam as unidades amostrais da réplica i e a última coluna, a média amostral da i-ésima réplica.

Vamos gerar o histograma que mostra a distribuição dos pesos médios dos recém nascidos em cada amostra, usando os comandos abaixo, em que primeiro convertemos a matriz M, mencionada anteriormente, em um “dataframe”, chamado de Mdf, para que seja aceita como argumento da função ggplot(). Em seguida, definimos que o eixo x representará a coluna chamada “Médias”, onde estão armazenados os pesos médios dos recém nascidos em cada amostra, e na função geom_histogram() que o eixo y indicará a densidade.

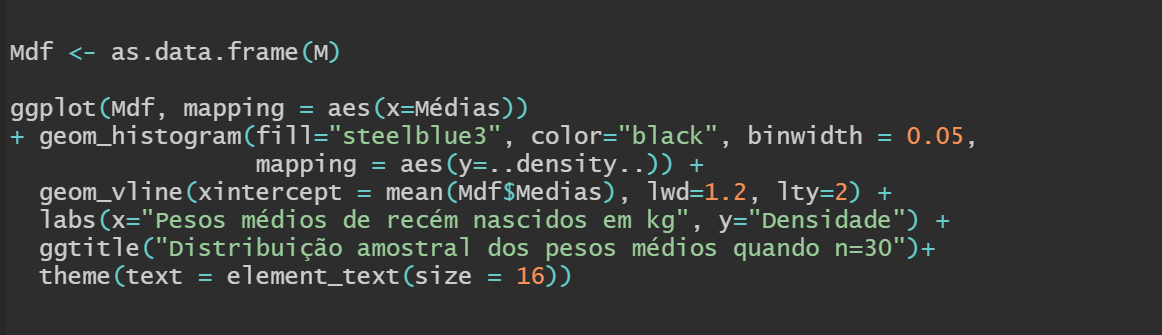
Assim, obteremos o histograma:

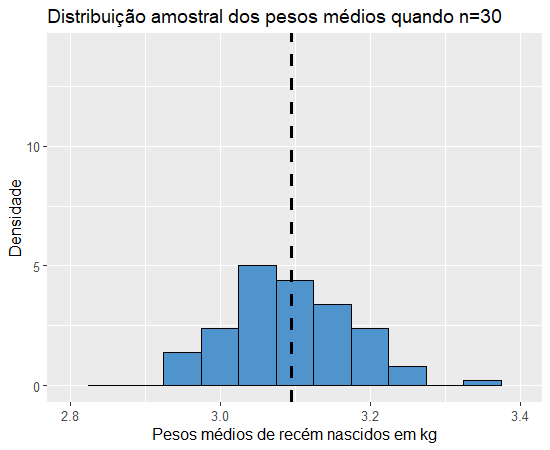
Nesse gráfico, a linha pontilhada representa a média dessa distribuição, ou seja, a média dos pesos médios de cada amostra, que foi 3.094585, e a sua variância foi de 0.009249179. Agora vamos analisar o que acontece com essas medidas quando mudamos o tamanho n das amostras.

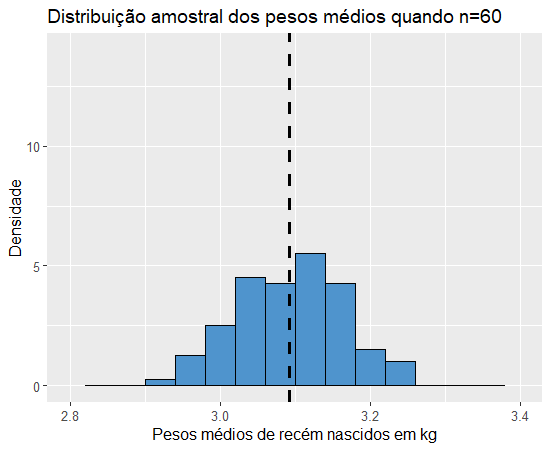
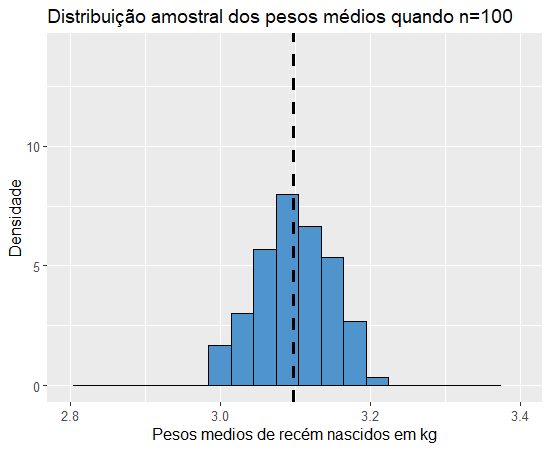
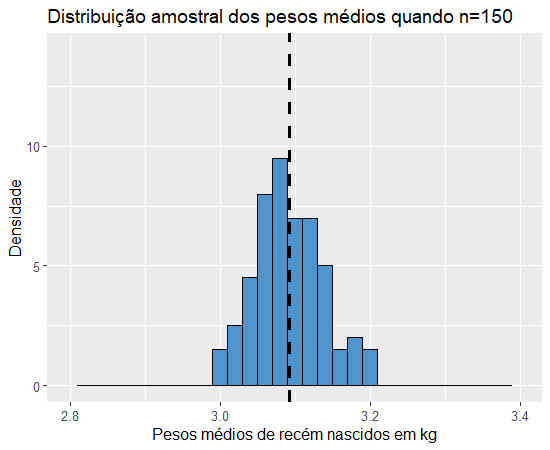
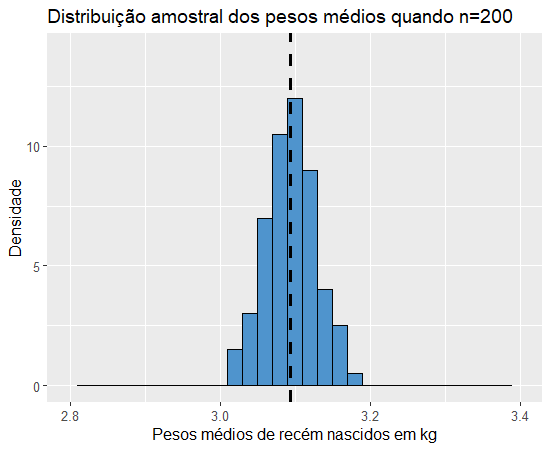
Observamos que as médias permanecem próximas a 3.1 em todos os gráficos e que quanto maior o tamanho amostral, mais concentrados estão os pesos médios de cada amostra em torno da média dos pesos médios (valor esperado do peso médio), ou seja, quanto maiores as amostrais, menor a variância do estimador. Isso faz bastante sentido se pensarmos da seguinte forma: pensando nessa população de 10000 pesos de recém nascidos, teremos um melhor estimador para o peso médio na população se analisarmos apenas um dos pesos obtidos por amostragem e tomarmos esse como estimador ou se fizermos o mesmo com uma amostra de 9999 pesos de bebês recém-nascidos? E se criássemos 1000 réplicas de tamanho 9999 dessa população, será que os pesos médios de cada réplica seriam muito diferentes uns dos outros?

A resposta para essa pergunta é bem intuitiva, quanto maior o tamanho da amostra, mais próximo o valor esperado do estimador estará do parâmetro, assim como, faz sentido que quanto maior o tamanho das amostras menor a variância do estimador, pois o peso médio de cada amostra estará mais próximo do peso médio da população. Essas propriedades podem ser demonstradas matematicamente. Sejam X1,X2,…,Xn uma amostra aleatória de uma variável aleatória cuja média seja μ e desvio-padrão seja σ, então a esperança da distribuição amostral da média é dada por:

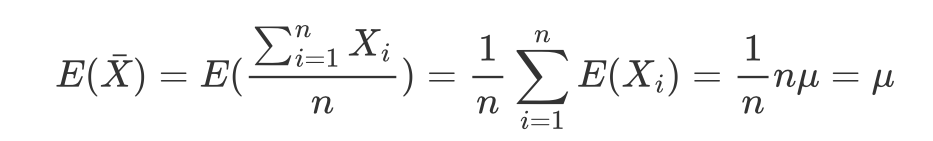
Sua variância pode ser usada calculando:

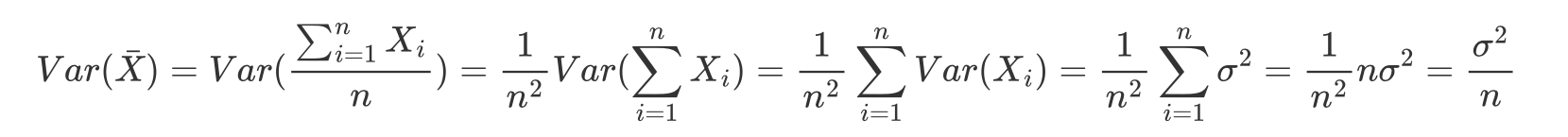
Note que os resultados acima independem da distribuição da variável aleatória. Além dessas propriedades, também podemos perceber que ao aumentarmos o tamanho das amostras, a distribuição amostral dos pesos médios se aproxima cada vez mais de uma distribuição normal de média μ e variância σ/2n. Porém, como foi mencionado quando criamos essa população no RStudio, a população formada pelo peso de recém nascidos apresenta teoricamente distribuição normal, sendo o histograma dos 10000 valores observados na população apresentado abaixo:

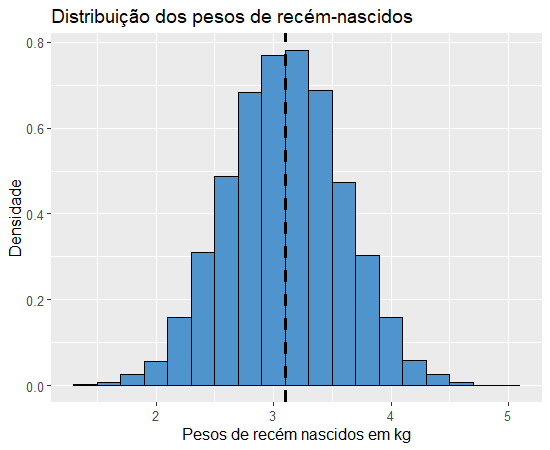
Pensando nisso, será que continua sendo verdade que a distribuição amostral se aproxima da normal à medida que n aumenta se a distribuição da variável na população não for normal?

Distribuição amostral da proporção

Para responder esse questionamento vamos usar outro exemplo. Temos 10000 gestantes e queremos avaliar a proporção que apresenta diabetes gestacional. Para cada gestante será atribuído o valor 1 se apresentar a doença ou 0 se não apresentar, ou seja, a presença ou não de diabetes gestacional em cada uma é uma variável aleatória representada pelo modelo Bernoulli. Já o total de grávidas com diabetes gestacional é a soma de todos os valores 1 e 0, ou seja, uma repetição de eventos independentes de Bernoulli, sendo expresso pelo modelo Binomial. Porém, estamos interessados na proporção dessa doença, que é dada como a média dos valores 1 e 0.

Primeiro vamos criar essa população no RStudio, que terá proporção de diabetes gestacional p=0.076, usando a função rbinom() como é mostrado abaixo:

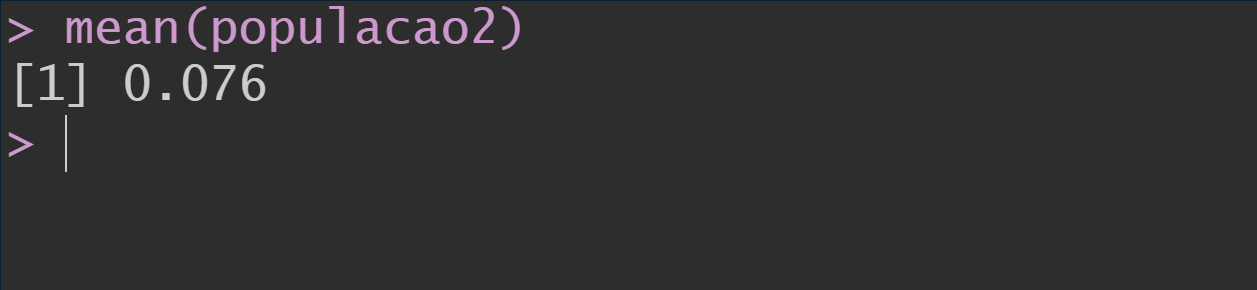
Supondo que não soubéssemos a proporção de gestantes com diabetes gestacional, vamos investigar o comportamento do estimador desse parâmetro usando a distribuição amostral da proporção com comandos similares aos do exemplo anterior:

Para diferentes tamanhos n de amostra teremos as seguintes distribuições:

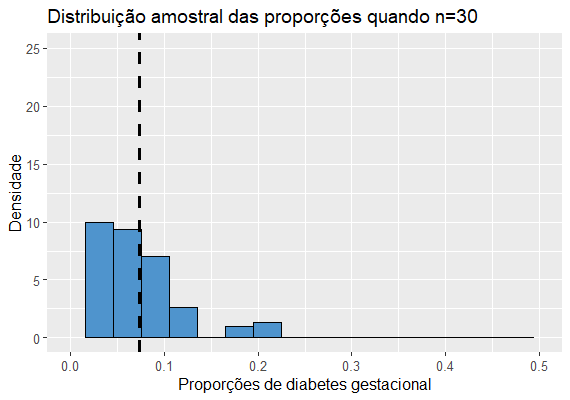
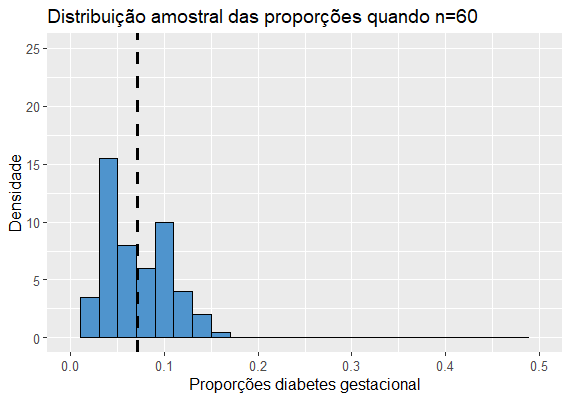
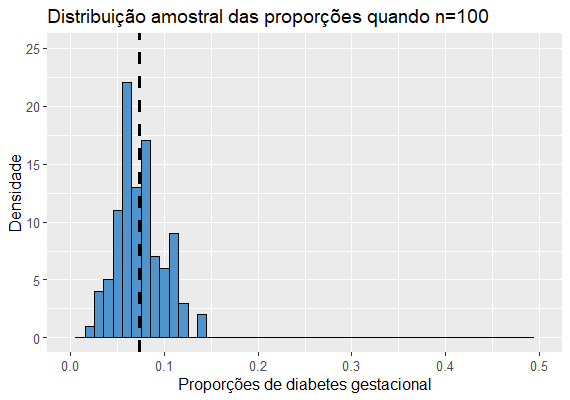
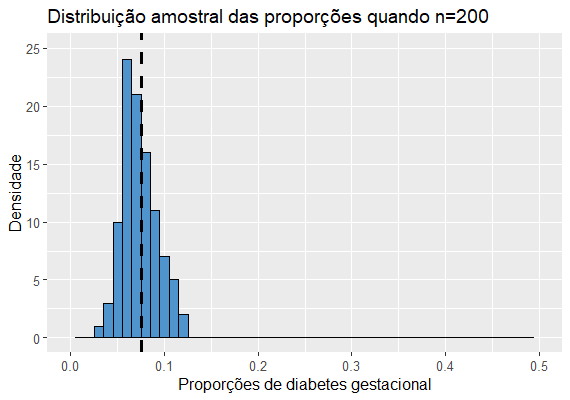
Notamos que as médias, que no caso representam a proporção média de grávidas com diabetes gestacional nas amostras, estão bem próximas de 0.076 em todos os histogramas.Também percebemos que quanto maior o tamanho amostral, mais concentradas estão as proporções em torno da média, ou seja, menor a variância, mais preciso é o estimador. Porém, quando falamos de proporção, a variância da distribuição amostral da proporção será diferente do que na distribuição amostral da média.

Assim, a esperança da distribuição amostral da proporção será:

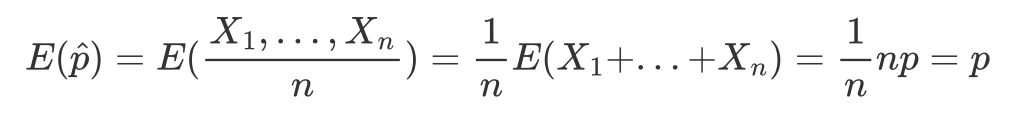
E a variância é dada por:

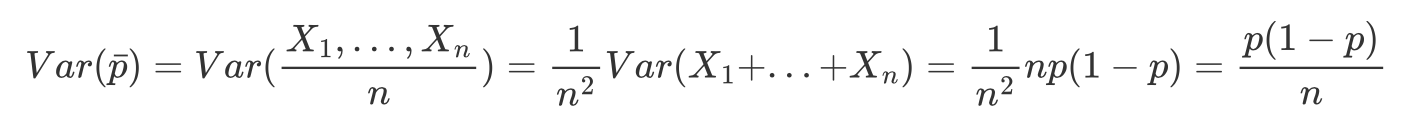
Observamos que ao aumentarmos o tamanho amostral, a distribuição das proporções de grávidas com diabetes gestacional nas amostras se aproxima cada vez mais de uma distribuição normal, apesar de seguir o modelo Binomial, o que responde o questionamento do início do exemplo. Essa propriedade é chamada Teorema do Limite Central, o qual afirma que, independente da distribuição da população, quanto maior o tamanho amostral, mais próxima será a distribuição amostral da média de uma distribuição normal. Lembrem-se que a proporção amostral é um caso particular da média amostral em que os valores observados na amostra contém apenas zeros e uns.

Conclusão

Bom, neste post focamos nas distribuições amostrais da média e da proporção, mas é importante ter em mente que podemos analisar a distribuição amostral de qualquer estatística/estimador, sendo algumas mais complexas. Aqui também deixamos disponível um link em Shiny onde é possível fazer simulações das distribuições amostrais da média e da proporção em diferentes populações. Esperamos que as informações aqui mostradas tenham ficado claras e de fácil entendimento. Para comentários, dúvidas ou sugestões entre em contato em observatorioobstetricobr@gmail.com.

Referências

MORETTIN, Pedro Alberto & BUSSAB, Wilton de Oliveira. Estatística básica. 8. ed. São Paulo: Saraiva, 2013, 548 p.

Departamento de Estatística Universidade Federal da Paraíba, Cálculo das Probabilidades e Estatística I, Versão 2013.