Durante as diversas etapas realizadas ao se ajustar um modelo regressão, é de extrema importância realizar análises de diagnóstico para ver se de fato o ajuste satisfaz certos pressupostos. No caso de um modelo de regressão linear normal, os pressupostos são erros independentes e normalmente distribuídos com média 0 e variância constante σ². A situação de variância constante recebe o nome de homoscedasticidade. A situação oposta, onde a variância dos erros muda de acordo com os valores das covariáveis, é denominada heteroscedasticidade. Dessa forma, se durante o ajuste de um modelo de regressão for verificado que algum desses pressupostos não foi atendido, é necessário pensar em maneiras de lidar com o problema encontrado.

O foco deste tutorial será justamente no problema da variância não constante e em modelagens alternativas para a variável resposta que vão além da distribuição normal. Em certas situações, uma transformação da variável resposta pode ser útil para contornar o problema dos resíduos heteroscedásticos, mas em outras, devido à própria natureza dos dados, teremos que utilizar ferramentas alternativas para nos auxiliar.

GAMLSS

Os GAMLSS (Generalized Additive Models for Location, Scale, and Shape), são uma classe de modelos que apresentam uma ampla variedade de distribuições para a variável resposta, trazendo maior flexibilidade ao ajuste (Rigby & Stasinopoulos (2005) e Rigby, et al.(2019)). Com ela podemos modelar todos parâmetros de uma regressão paramétrica, ou seja, além da modelagem da média (parâmetro de locação), é possível também considerar a variância (parâmetro de escala), a assimetria e a curtose (parâmetros da forma) como funções das covariáveis.

Sua implementação na linguagem R é dada pelo pacote de mesmo nome. Com ele já instalado  e carregado, ao digitar  ?gamlss ou help(gamlss) podemos ver as diversas distribuições que podemos considerar durante as modelagens. Cada distribuição tem seus parâmetros específicos e todos eles podem ser modelados.

No R

Será utilizada uma base com dados anonimizados referentes a medidas ultrassonográficas de gestantes diabéticas ou com diabetes gestacional registradas na Clínica Obstétrica do Hospital das Clínicas da Faculdade de Medicina da Universidade de São Paulo (HC-FMUSP). Nos códigos, essa base será chamada de “dados_7”.

Nos exemplos serão ajustados diversos modelos de regressão que relacionam o peso estimado (PEstima) com o peso observado no parto (pesoRN). O objetivo aqui será verificar a eficácia das estimações para o peso ao nascer quando se utiliza o peso fetal registrado em uma ultrassom próxima ao parto (ou seja, verificar se as estimações são fiéis aos pesos de nascimento observados). Sendo assim, espera-se que a relação entre as variáveis seja a mais linear possível.

Primeiramente ajustaremos um modelo linear normal com a função lm().

> modelo_1 = lm(data=dados_7,formula=pesoRN~PEstima)
> summary(modelo_1)
Call:
lm(formula = pesoRN ~ PEstima, data = dados_7)
Residuals:
      Min        1Q    Median        3Q       Max 
-0.201544 -0.023948  0.000908  0.024867  0.117846 
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  0.31511    0.05819   5.415  1.1e-07 ***
PEstima      0.91070    0.01679  54.251  < 2e-16 ***
--- 
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.03909 on 371 degrees of freedom
Multiple R-squared:  0.8881,	Adjusted R-squared:  0.8878 
F-statistic:  2943 on 1 and 371 DF,  p-value: < 2.2e-16

Na saída Residuals são mostradas algumas medidas-resumo da distribuição dos resíduos, note pela mediana (Median) que a distribuição dos resíduos está centrada próxima de zero e pelos quartis (1Q e 3Q) que ela é simétrica. Na saída Coefficients são apresentados os resultados do teste-t para os coeficientes do modelo (testa se eles são iguais a zero ou não). Observa-se que o coeficiente da covariável PEstima foi significativo (p<0.05). Além disso, os coeficientes de determinação (Multiple R-squared) e de determinação ajustado (Adjusted R-squared) apresentaram valores próximos de um, isso significa que grande parte da variabilidade do pesoRN é explicada pelo modelo proposto. Logo em seguida são mostrados alguns resultados da análise de variância (ANOVA), como nesse caso estamos usando somente uma covariável, o teste-f é equivalente ao teste-t usado para testar o coeficiente de inclinação da variável PEstima.  Os resultados obtidos nessa primeira parte do ajuste foram satisfatórios, sendo assim, prosseguiremos com as análises.

O foco será agora ver o comportamento dos resíduos do modelo, tal etapa é denominada análise residual. Existem diversos tipos de gráficos e testes estatísticos que podem ser utilizados nessa etapa para observar, a partir dos resíduos (que servem como estimativas para os erros), se os pressupostos do modelo foram atendidos.

Construindo pelo gamlss o mesmo modelo da função lm(), teremos acesso a uma série de análises gráficas úteis para essa parte da modelagem. Primeiro vamos rodar o modelo.

> modelo_1=gamlss(data=dados_7,formula=pesoRN~PEstima,family=NO)
GAMLSS-RS iteration 1: Global Deviance = -1361.926 
GAMLSS-RS iteration 2: Global Deviance = -1361.926

O argumento family serve para indicar a distribuição considerada na modelagem, nesse caso estamos considerando a normal. Para ver quais coeficientes foram significativos basta usar summary(), assim como se faz com a lm(). A função plot() também pode ser usada com o pacote, como é mostrado abaixo.

> plot(modelo_1)
******************************************************************
Summary of the Quantile Residuals
mean = -2.943021e-16 
variance = 1.002688 
coef. of skewness = -0.5064871 
coef. of kurtosis = 5.094336 
Filliben correlation coefficient = 0.9883316 
******************************************************************

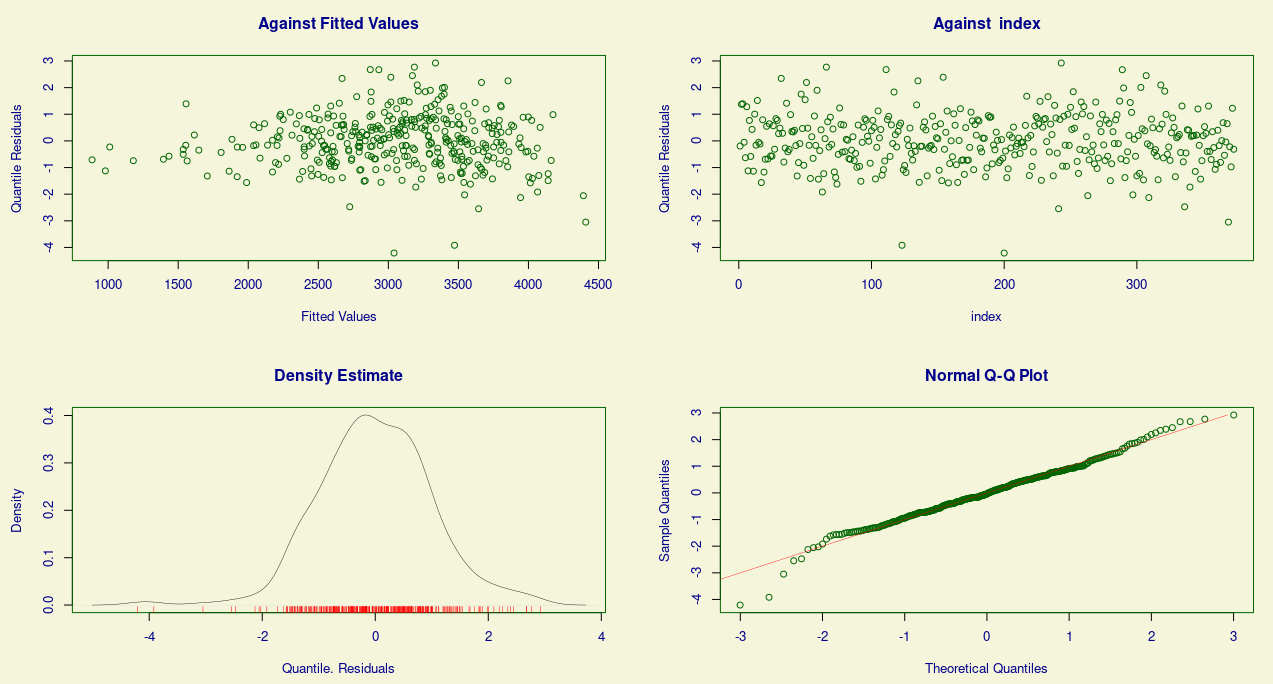
Os resíduos que agora foram considerados são os resíduos quantílicos. No output da função são mostradas algumas medidas descritivas para eles como assimetria (skewness) e curtose (kurtosis). Repare que no gráfico Against Fitted Values, os resíduos não estão dispersos aleatoriamente por todo o plano cartesiano. Os resíduos correspondentes aos menores valores ajustados variam menos entre si do que os resíduos dos valores ajustados mais altos. É fácil perceber um padrão no comportamento deles, esse padrão acaba formando no gráfico um desenho que lembra o formato de um megafone. Esse tipo de situação é típica de resíduos heteroscedásticos. Sendo assim, um dos pressupostos para o modelo linear normal foi descumprido. Vale lembrar que existem diversos testes estatísticos para verificar se um determinado modelo é homoscedástico ou não. Como o intuito aqui é ilustrar como a heteroscedásticidade afeta a nossa análise residual (afetando consequentemente as estimações do nosso modelo de regressão), estamos realizando nossas análises de maneira bem visual.

Nessa etapa, poderíamos utilizar uma transformação da variável resposta para tentar contornar o problema. O gráfico de Box-Cox, implementado no R pela função boxcox(modelo_ajustado), pode nos auxiliar na escolha de uma transformação na variável resposta, porém ele não funciona com os objetos gamlss(modelo_ajustado). Sendo assim, deveríamos testar algumas transformações e ver se elas conseguem atenuar o problema encontrado. Como o modelo que estamos ajustando nesse primeiro momento é o linear normal, vamos rodá-lo novamente pela função lm() e ver qual transformação seria sugerida.

> modelo_1 = lm(data=dados_7,formula=pesoRN~PEstima)
> boxcox(modelo_1,seq(0,2,0.2))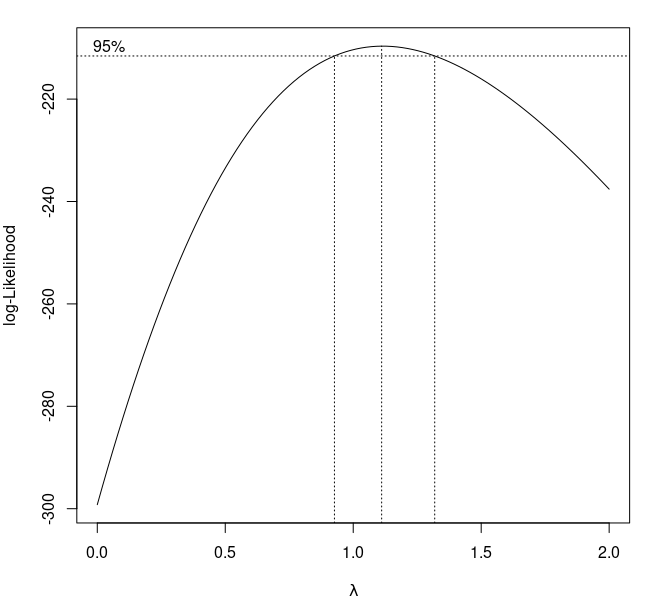

Como o nosso foco são nos gamlss, não será detalhado como funciona essa transformação aqui (ver Box GEP, Cox DR (1964) An analysis of transformations. J Roy Stat Soc, Ser B 26:211–252), mas de maneira bem resumida, como o intervalo para o λ engloba o valor 1, então não será necessário transformar a variável resposta (pesoRN). Vamos então partir para modelagens alternativas ao modelo de regressão linear normal.

Chamaremos esse novo ajuste de modelo_2. Para introduzir a variância não constante no modelo basta utilizar argumento sigma.formula = pesoRN~PEstima. Vale lembrar que nosso objetivo aqui é simplesmente verificar se a relação entre duas variáveis é linear, sendo assim, temos somente uma covariável. Em uma situação mais prática, com diversas covariáveis, poderíamos utilizar a função stepGAIC(nome_do_modelo,what=sigma) para rodar o algoritmo stepwise que nos auxiliará na seleção de um bom modelo para a variância, o mesmo poderia ser feito para qualquer outro parâmetro mudando o valor do argumento what. Para ver os parâmetros presentes na distribuição escolhida, basta usar gamlss.family(nome_da_distribuição).

> gamlss.family(NO)

GAMLSS Family: NO Normal 
Link function for mu : identity 
Link function for sigma: log 
> gamlss.family(TF)

GAMLSS Family: TF t Family 
Link function for mu : identity 
Link function for sigma: log 
Link function for nu : log

Vamos então rodar o nosso segundo modelo.

> modelo_2=gamlss(data=dados_7,formula=pesoRN~PEstima,
sigma.formula=pesoRN~PEstima,family=NO)
GAMLSS-RS iteration 1: Global Deviance = 5219.124 
GAMLSS-RS iteration 2: Global Deviance = 5215.638 
GAMLSS-RS iteration 3: Global Deviance = 5215.48 
GAMLSS-RS iteration 4: Global Deviance = 5215.475 
GAMLSS-RS iteration 5: Global Deviance = 5215.475

> summary(modelo_2)
******************************************************************
Family:  c("NO", "Normal") 

Call:  gamlss(formula = pesoRN ~ PEstima, sigma.formula = pesoRN ~  
    PEstima, family = NO, data = dados_7) 

Fitting method: RS() 

------------------------------------------------------------------
Mu link function:  identity
Mu Coefficients:
             Estimate   Std. Error  t value  Pr(>|t|)    
(Intercept)  227.70650  54.01412    4.216    3.14e-05 ***
PEstima      0.93716    0.01903     49.248   < 2e-16 *** ---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------
Sigma link function:  log
Sigma Coefficients:
             Estimate   Std. Error  t value  Pr(>|t|)    
(Intercept)  4.833e+00  1.848e-01   26.154   < 2e-16 ***
PEstima      2.456e-04  6.017e-05   4.082    5.48e-05 *** ---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
------------------------------------------------------------------
No. of observations in the fit:  373 
Degrees of Freedom for the fit:  4
      Residual Deg. of Freedom:  369 
                      at cycle:  5   
Global Deviance:     5215.475 
            AIC:     5223.475 
            SBC:     5239.161 
******************************************************************

Pelo output do summary do modelo temos informações como os coeficientes do modelo, as funções de ligação usadas (mu.link e sigma.link), quantidade de observações (No. of observations in the fit) e as métricas para comparar os modelos (AIC, SBC e global.deviance). Na saída Mu coefficients são mostrados os resultados dos testes dos coeficientes da modelagem para a média. Já no caso de Sigma coefficients, são mostrados os resultados dos testes dos coeficientes da modelagem para a variância. Repare que todos foram significativos (p<0.05), vamos agora às análises dos resíduos.

> plot(modelo_2)
******************************************************************
Summary of the Quantile Residuals
mean = -0.004360303 
variance = 1.002669 
coef. of skewness = -0.07081213 
coef. of kurtosis = 4.017129 
Filliben correlation coefficient = 0.9937761 
******************************************************************

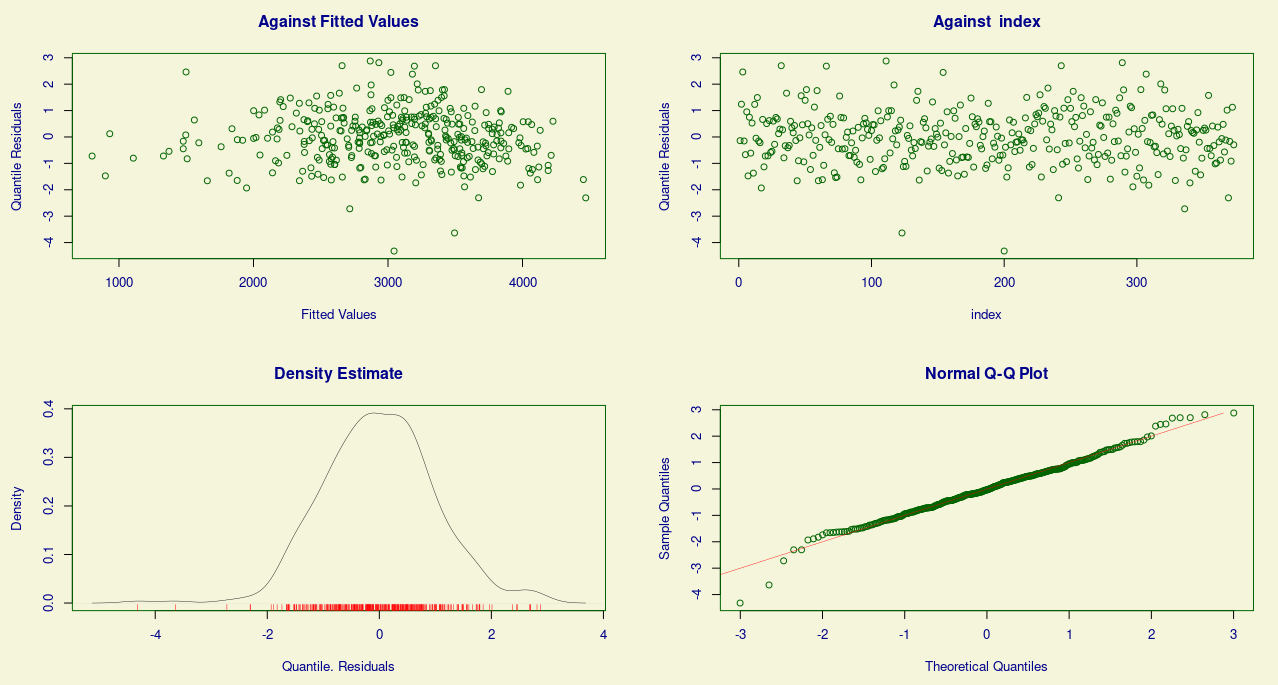
Aparentemente o problema da variância não constante foi atenuado com essa modelagem, entretanto, pelas análises acima, percebemos a presença de caudas pesadas em sua distribuição (curtose = 4.017129), o ideal é que as caudas tenham curtose bem próxima de 3, valor da curtose de uma normal. Logo, distribuições com caudas mais pesadas devem ser consideradas na modelagem.

Vamos então tentar usar a distribuição T-Student (foi mudado o argumento de family=NO para family=TF).

> modelo_3=gamlss(data=dados_7,formula=pesoRN~PEstima,
sigma.formula=pesoRN~PEstima,family=TF)
GAMLSS-RS iteration 1: Global Deviance = 5212.2 
GAMLSS-RS iteration 2: Global Deviance = 5208.431 
GAMLSS-RS iteration 3: Global Deviance = 5208.251 
GAMLSS-RS iteration 4: Global Deviance = 5208.244 
GAMLSS-RS iteration 5: Global Deviance = 5208.244  > summary(modelo_3)
******************************************************************
Family: c("TF", "t Family")

Call: gamlss(formula = pesoRN ~ PEstima, sigma.formula = pesoRN ~ 
PEstima, family = TF, data = dados_7)

Fitting method: RS()

------------------------------------------------------------------
Mu link function: identity
Mu Coefficients:
            Estimate   Std. Error  t value  Pr(>|t|) 
(Intercept) 219.07312  52.90693    4.141    4.3e-05 ***
PEstima     0.93992    0.01861     50.513   < 2e-16 *** ---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------
Sigma link function: log
Sigma Coefficients:
            Estimate   Std. Error  t value  Pr(>|t|) 
(Intercept) 4.730e+00  2.083e-01   22.71    < 2e-16 ***
PEstima     2.442e-04  6.653e-05   3.67     0.000278 *** ---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 ------------------------------------------------------------------
Nu link function: log 
Nu Coefficients:
            Estimate  Std. Error  t value  Pr(>|t|) 
(Intercept) 2.352     0.454       5.181    3.64e-07 *** ---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 
------------------------------------------------------------------
No. of observations in the fit: 373 
Degrees of Freedom for the fit: 5
Residual Deg. of Freedom: 368 
at cycle: 5  Global Deviance: 5208.244 
AIC: 5218.244 
SBC: 5237.852 
******************************************************************

Em Nu Coefficients temos a estimativa para o parâmetro grau de liberdade, repare que seu valor estimado foi bem baixo, reforçando assim que a utilização de uma normal não seja tão boa para esse caso (com valores muito altos a distribuição T-Student aproxima para a normal). Vamos observar o plot() do modelo.

> plot(modelo_3)
******************************************************************
Summary of the Quantile Residuals
mean = -0.001962187 
variance = 1.002563 
coef. of skewness = 0.01885042 
coef. of kurtosis = 3.008914 
Filliben correlation coefficient = 0.9979069 
******************************************************************

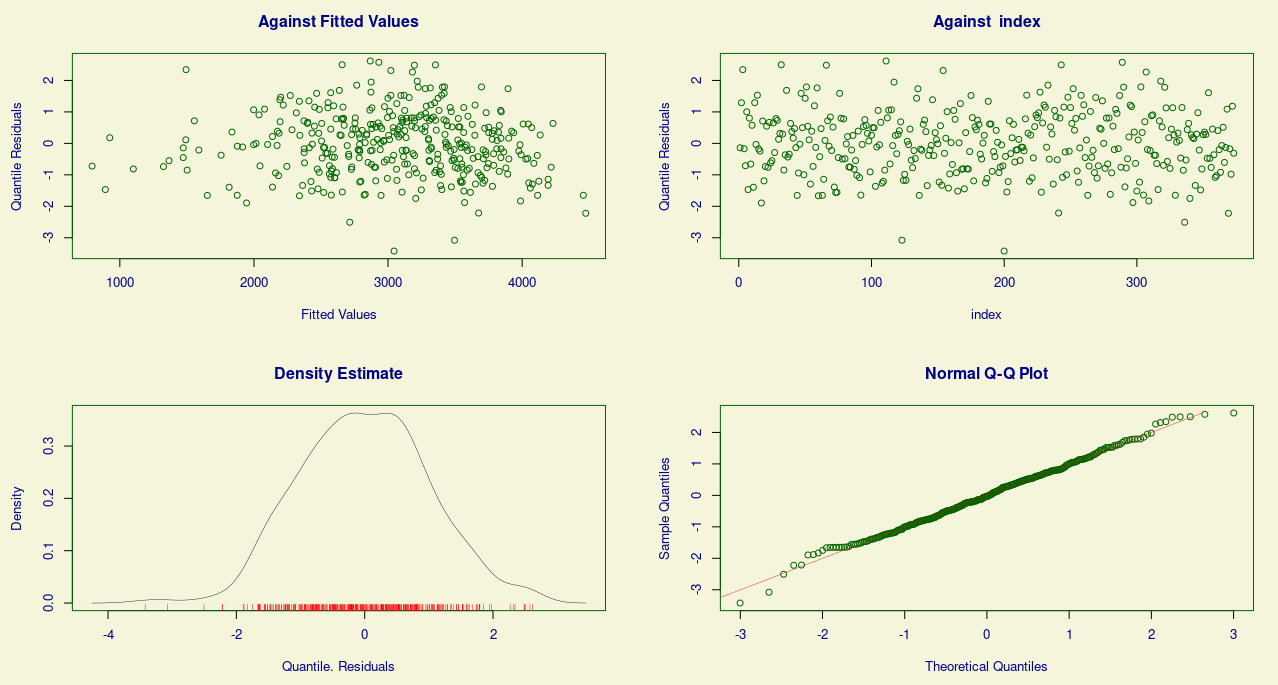
Perceba que além dos resíduos terem se tornado ainda mais homoscedásticos, o problema das caudas pesadas em sua distribuição também conseguiu ser contornado. Logo, será esse o modelo escolhido.

Voltando ao objetivo do nosso ajuste, ver o quão linear é a relação entre as duas variáveis, basta observar no summary(modelo_3) que o coeficiente de inclinação do modelo (no caso o coeficiente da média, μ) foi significativo e teve um valor estimado dado por 0.93992 (Quanto mais próximo do valor 1, mais linear é a relação).

Referências

Stasinopoulos, D. Mikis; Rigby,Robert A. Generalized Additive Models for Location Scale and Shape (GAMLSS) in R. Journal of Statistical Software, JSS. Dezembro 2007.