Introdução

Com o aumento da capacidade de armazenamento e processamento de dados, a exploração e análise desses dados exigem não apenas métodos estatísticos, mas também técnicas computacionais. A área de Machine Learning (ML; Aprendizado de Máquina, em português) resulta da integração entre Estatística e Ciência da Computação, utilizando modelos estatísticos combinados com algoritmos computacionais para extrair informações valiosas de conjuntos de dados com muitas observações e/ou variáveis. ML pode ser supervisionado ou não supervisionado. Aqui, focamos no ML supervisionado, que envolve o treinamento de modelos com dados rotulados, onde a resposta correta (ou variável resposta, também chamada de label, output ou desfecho) é conhecida. O objetivo é fazer previsões ou classificações, aprendendo a relação entre as variáveis preditoras (conhecidas como input, features, variáveis explicativas ou covariáveis) e a variável resposta a partir de exemplos passados.

Em ML supervisionado, uma distinção entre modelo explicativo – alguns autores chamam de modelo inferencial – e modelo preditivo precisa ser feita. Quando o objetivo está na interpretação dos parâmetros envolvidos do modelo e na testagem de hipóteses para entender a relação entre as covariáveis e a variável resposta, um modelo com o intuito explicativo é ajustado. Já no modelo preditivo, o foco está na construção de um modelo para predizer novas observações.

Historicamente, modelos com o intuito explicativo são amplamente utilizados na área da saúde para entender, por exemplo, que a exposição a um dado fator tem tantas vezes mais chance de ter o desfecho de interesse, e que essa relação é significativa do ponto de vista estatístico e clínico. Um exemplo na área da medicina obstétrica foi um estudo realizado para avaliar se o uso de progesterona comercial em gestantes com colo curto diminui o risco de prematuridade (parto ocorrer antes de 37 semanas gestacionais). Como resultado de um ensaio clínico randomizado, duplo-cego e controlado por placebo, observou-se que a chance de prematuridade é diminuída em 60% com o uso da progesterona[1]. Além desse estudo realizado no Brasil, outros pesquisadores replicaram o mesmo estudo em outras partes do mundo e obtiveram resultados reprodutíveis (que chegaram a mesma conclusão) e uma metanálise (análise combinada de todos os estudos)[2] também foi realizada, concluindo que há indícios favoráveis ao uso de progesterona comercial em gestações com colo curto. Com base nas evidências científicas apresentadas, virou então protocolo obstétrico o uso de progesterona comercial em gestantes identificadas com colo curto para diminuir o risco de parto precoce.

Nos últimos anos, tem surgido o interesse em também realizar predições de desfechos na área da saúde e modelos preditivos têm sido cada vez mais utilizados. Como exemplo na área da medicina obstétrica, desejou-se construir um modelo para predizer, no momento do diagnóstico de diabetes gestacional, se uma gestante faria uso de insulina em algum momento anterior ao parto com base em informações clínicas, exames laboratoriais e histórico obstétrico e familiar[3]. Assim, uma gestante com 35 anos, obesa, com histórico familiar de diabetes, com histórico de diabetes gestacional anterior e que obteve 100mg/dL de glicemia de jejum no momento do diagnóstico da diabetes gestacional na gestação atual tem uma probabilidade de uso de insulina estimada de 70,9%, obtida por meio do modelo construído nesse estudo. Como essa probabilidade é maior do que o ponto de corte considerado, há então alta chance dessa gestante fazer o uso da insulina.

Ainda que o intuito do ajuste do modelo seja de predição, os pesquisadores também podem ter o interesse em entender as variáveis escolhidas no modelo e discutir a influência delas na tomada de decisões obtidas pelo modelo preditivo. Há modelos estatísticos que podem ser considerados tanto com o intuito preditivo quanto inferencial, uma vez que seus parâmetros podem ser interpretados naturalmente, o que chamamos de modelos explicáveis. O modelo de regressão logística é um exemplo de modelo explicável, em que o exponencial de um parâmetro é a razão de chances. No exemplo das pacientes com diabetes gestacional, foi ajustado um modelo de regressão logística para o uso de insulina (“sim” ou “não”), em que a variável indicadora de diabetes gestacional anterior foi selecionada para esse modelo preditivo. Por usar um modelo explicável, foi possível verificar, por exemplo, que a chance de fazer uso de insulina quando presente diabetes em uma gestação anterior é 2,8 vezes a chance de fazer uso de insulina sem diabetes anterior ( 2,8=e^1,03, em que 1,03 é a estimativa do parâmetro associado ao indicador de diabetes gestacional prévia).

Mesmo nos casos de utilização de modelos explicáveis, é importante decidir qual o intuito do ajuste do modelo, já que o processo de modelagem é diferente a depender da intenção. Quando o intuito é inferencial, as escolhas feitas durante o processo de modelagem são pautadas em medidas que avaliam a relação de explicação entre as variáveis. Já com o objetivo de predição, as escolhas no processo de modelagem são guiadas por medidas de desempenho preditivo, como a acurácia (capacidade de acertar ou errar uma predição dentro de um limiar aceitável).

É comum se deparar com aplicações em que as escolhas realizadas foram guiadas com o intuito preditivo e o pesquisador interpreta os parâmetros resultantes e também o contrário, ou seja, ajustando um modelo explicativo que também é usado para predição. No entanto, isso pode não ser uma boa estratégia. No primeiro cenário, pode acontecer de ter uma variável no modelo que aumenta o seu poder preditivo mas que não faz nenhum sentido inferencial; no segundo cenário, o modelo explicativo utilizado para fazer predição não apresentar o maior poder preditivo entre todos os possíveis de um conjunto de modelos preditivos.

Quando o objetivo for a predição, há aqueles explicáveis, já discutidos anteriormente, e os modelos não explicáveis, conhecidos como modelos caixa-preta (algoritmos cujo funcionamento interno não pode ser facilmente explicado). O modelo escolhido será aquele com melhor desempenho preditivo e esse “melhor” pode ser de um modelo não explicável. Contudo, conhecer o porquê do desfecho pode ajudar a entender mais sobre o problema, sobre os dados e em quais situações esse modelo não é razoável. Em outras palavras, mesmo que em um primeiro momento o objetivo do modelo seja preditivo, há também a importância em se explicar as decisões tomadas pelo modelo. Além de possibilitar testar se pequenas alterações nas covariáveis levam a grandes alterações nas predições, é mais fácil para as pessoas confiarem em um sistema que explique suas decisões e julgarem se estas foram baseadas em um viés demográfico aprendido (por exemplo, racial).

Para facilitar, então, o aprendizado e satisfazer a curiosidade sobre o motivo de certas predições ou comportamentos, métodos de interpretabilidade global e individual podem ser aplicados a qualquer modelo preditivo previamente ajustado. Um desses métodos é o SHAP, que estuda o impacto das covariáveis na saída do modelo e explica globalmente e individualmente as decisões do modelo[4]. O novo escore de crédito da Serasa, por exemplo, apresenta um campo que explica os fatores que aumentam e diminuem a pontuação obtida pela pessoa física (PF). Essa explicação individual (para cada PF) é obtida, possivelmente, pelo SHAP.

Neste post, o método de interpretabilidade SHAP, em sua versão global e individual, será discutido em uma aplicação da área da medicina obstétrica resultante de pesquisas realizadas pelo Departamento de Obstetrícia e Ginecologia da Faculdade de Medicina da Universidade de São Paulo (DOG-FMUSP). A partir de um modelo preditivo XGBoost previamente ajustado, em que seu objetivo foi prever se uma gestante diagnosticada com diabetes gestacional precisaria usar insulina em algum momento anterior ao parto, veremos como interpretar, por meio de gráficos, suas decisões.

Mas, antes, vamos entender o que está por detrás das cortinas do SHAP?

Shapley e SHAP

Desenvolvido por Shapley (2016)[5], o Valor de Shapley é um conceito da Teoria dos Jogos que descreve como distribuir, de forma justa, uma premiação aos jogadores de um time de acordo com a contribuição individual de cada um no resultado final de um jogo. A ideia é imaginar que os jogadores são incluídos aleatoriamente ao time um a um, e cada vez que um novo jogador se junta à equipe, ele recebe um valor relacionado à sua contribuição. Essa contribuição, que é o valor de Shapley propriamente dito, é a média de todas as combinações possíveis, em todas as ordens possíveis de adesão, que contém e não contém determinado jogador. No contexto de aprendizado de máquina, por sua vez, podemos traduzir o “jogo” como o modelo preditivo, os “jogadores” como as covariáveis e o “resultado final” como a predição. O valor de Shapley é então definido pela média ponderada, por uma constante normalizadora, da soma de todas as diferenças possíveis entre os modelos treinados com (ƒ_S∪{j}) e sem (ƒ_s) a j-ésima covariável sob investigação.

Matematicamente, temos que

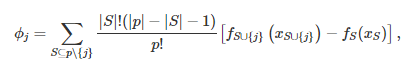
em que p é o conjunto de todas as covariáveis e x_s é o vetor com todos os valores de entrada das covariáveis do subconjunto S.

O valor de Shapley encontrado pode ser interpretado como o quanto a inclusão da j-ésima covariável contribuiu para a predição de uma determinada observação x em relação à predição média feita para todos os dados. A contribuição é considerada “positiva” (valor de Shapley positivo) quando a variável aumenta a chance de ocorrer o desfecho de interesse (por exemplo, saber se a gestante usará insulina) e é considerada “negativa” (valor de Shapley negativo) quando a variável diminui a chance de ocorrer tal desfecho.

É fato que a teoria sólida por trás do Valor de Shapley fez com ele fosse considerado um dos métodos mais completos para explicar modelos de aprendizado de máquina. No entanto, o alto custo computacional (devido a todas permutações possíveis de subconjuntos de variáveis) e a limitação de intepretar modelos mais complexos (como os de redes neurais profundas) se tornaram seus incovenientes. Assim, Lundberg & Lee (2017)[6] propuseram, como alternativa, o método Explicações Aditivas de Shapley, popularmente conhecido como “SHAP” (do inglês, SHapley Additive exPlanations), uma implementação unificada de vários métodos para interpretar as decisões de qualquer modelo não interpretável. Uma inovação que o SHAP traz, por exemplo, é representar o valor de Shapley como um modelo cuja explicação é dada por uma função linear de variáveis binárias:

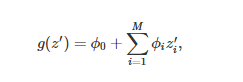
em que g é o modelo de explicação, z′∈{0,1}^p, p sendo o número de covariáveis de entrada, e  ϕ_i ∈ ℝ.

Na prática, esses modelos, que são conhecidos como modelos de atribuição aditiva, atribuem um efeito  ϕ_i para cada covariável de tal maneira que a soma de todos os efeitos se aproximarão da resposta  ƒ(x) do modelo original a ser explicado.

Uma outra (grande) vantagem do SHAP em relação ao Valor de Shapley é sua PODEROSA – e belíssima – visualização gráfica. Para o caso em que a intenção do pesquisador seja interpretar globalmente as predições, existem, por exemplo, os gráficos de importância, de resumo e de dependência SHAP. Já para o caso em que sua pretensão seja fazer interpretações individuais, pode-se utilizar os gráficos de cascata e de força SHAP.

Porém, num primeiro momento, interpretá-los pode ser uma tarefa não tanto intuitiva assim. Por isso, a ideia deste post é justamente explicar como interpretar cada um desses cinco gráficos de SHAP na ín-te-gra. Aguarde as próximas seções e leia Molnar (2020)[4] para saber sobre o método SHAP em detalhes!

Obs.: para os leitores curiosos, os gráficos que aqui serão apresentados foram construídos utilizando os pacotes {shapviz} + {ggplot2}, do R, e o pacote {shap}, do Python.

Interpretabilidade global

O objetivo dos métodos de interpretação global é descrever o comportamento esperado de um modelo de aprendizado de máquina com base na média dos resultados de todos os desfechos, obtida segundo a distribuição total de valores de cada uma das covariáveis consideradas. Com o SHAP, isso é alcançado agregando os valores de SHAP de todos os indivíduos da amostra.

Gráfico de importância SHAP

No gráfico de importância SHAP, conseguimos identificar a contribuição média de cada covariável, dada pela média do valor absoluto de SHAP. Ao tomar a média do valor absoluto de SHAP, o resultado é expresso em unidade intuitivamente interpretável. Em nossa aplicação, por exemplo, a média dos valores absolutos de SHAP significa, em média, o quanto cada covariável influenciou na prescrição ou não de insulina antes do parto. A magnitude das contribuições, geralmente, é representada por barras horizontais, que são ordenadas no eixo y de forma decrescente. As covariáveis com as maiores contribuições têm mais impacto sobre as decisões do modelo.

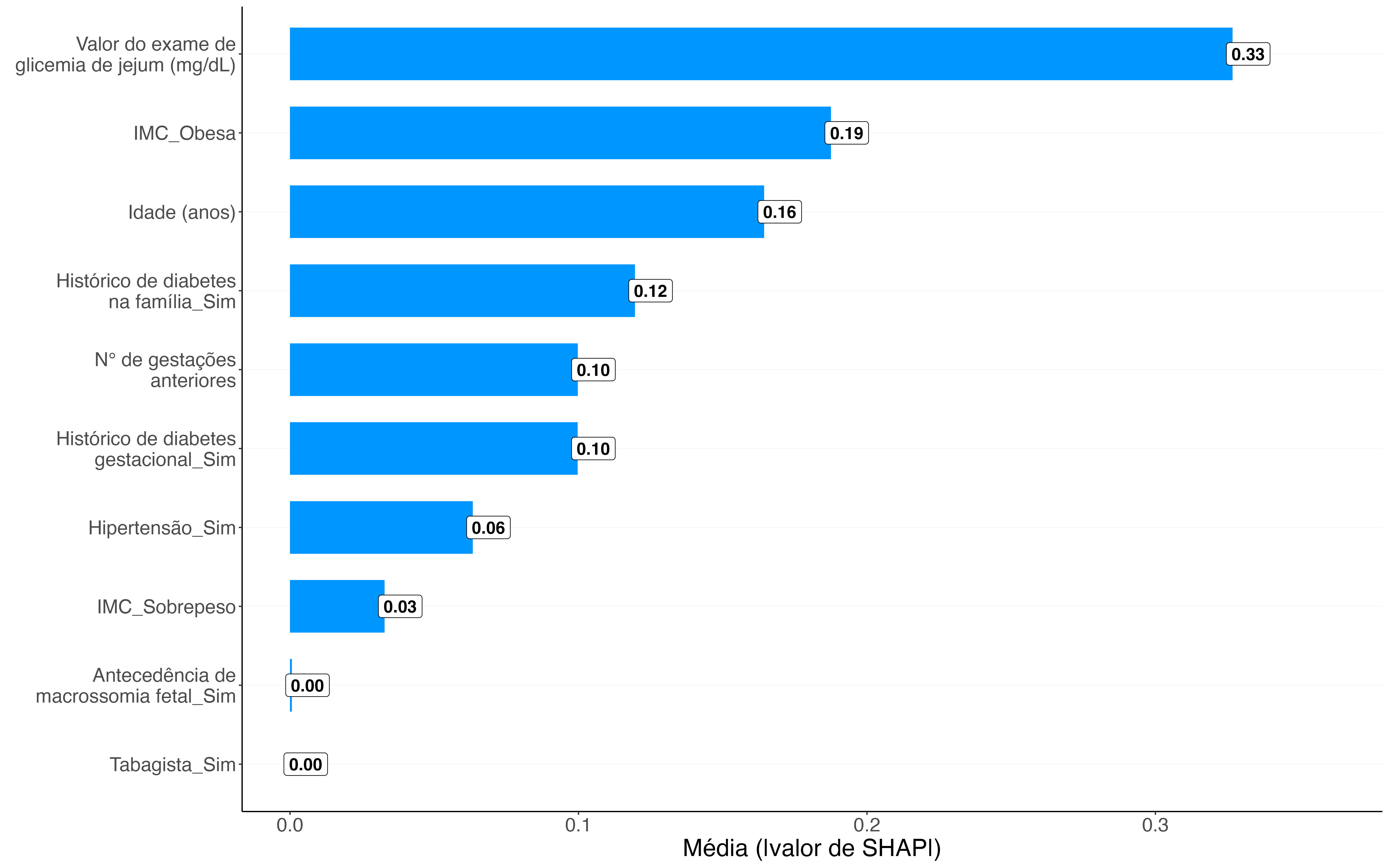
Figura 1: Gráfico de importância SHAP para dados de diabetes gestacional do HCFMUSP.

As principais características a serem observadas na Figura 1, portanto, é a ordenação das covariáveis e o tamanho (a magnitude) das barras. Assim, o valor do exame de glicemia de jejum, a obesidade e a idade foram as variáveis mais influentes nas decisões do modelo, alterando, em média, a probabilidade predita de receitar insulina à gestante em 0,33%, 0,19% e 0,16% pontos percentuais, respectivamente. Na contramão, estão antecedência de macrossomia fetal (categoria: “sim”) e tabagista (categoria: “sim”), pois com nenhum ou quase nenhum percentual de contribuição foram as covariáveis sem qualquer efeito nos resultados – a contribuição de antecedência de macrossomia fetal não foi necessariamente zero, e por isso é mostrada uma pequena, quase nula, porção de barra.

Gráfico de resumo SHAP

Para interpretar globalmente os resultados do modelo XGBoost proposto, também podemos utilizar o gráfico de resumo SHAP. Nesse gráfico, as covariáveis de entrada são ordenadas no eixo y de forma decrescente, de cima para baixo, de acordo com os valores absolutos médios de SHAP – mesma informação trazida pelo gráfico de importância visto anteriormente. Em cada uma dessas covariáveis, cada ponto é uma observação, e os pontos são distribuídos horizontalmente ao longo do eixo x segundo seu respectivo valor de SHAP – quando a densidade em um valor de SHAP é alta, os pontos se dispersam verticalmente. A barra de cores representa os valores brutos das covariáveis para cada ponto no gráfico: se para uma determinada covariável o valor é alto, o ponto é colorido por algum tom de vermelho; se o valor é baixo, o ponto é então preenchido por algum tom de azul. A distribuição de cores na horizontal permite entender naturalmente a relação geral de cada covariável com os valores de SHAP (e, logo, com os resultados preditos).

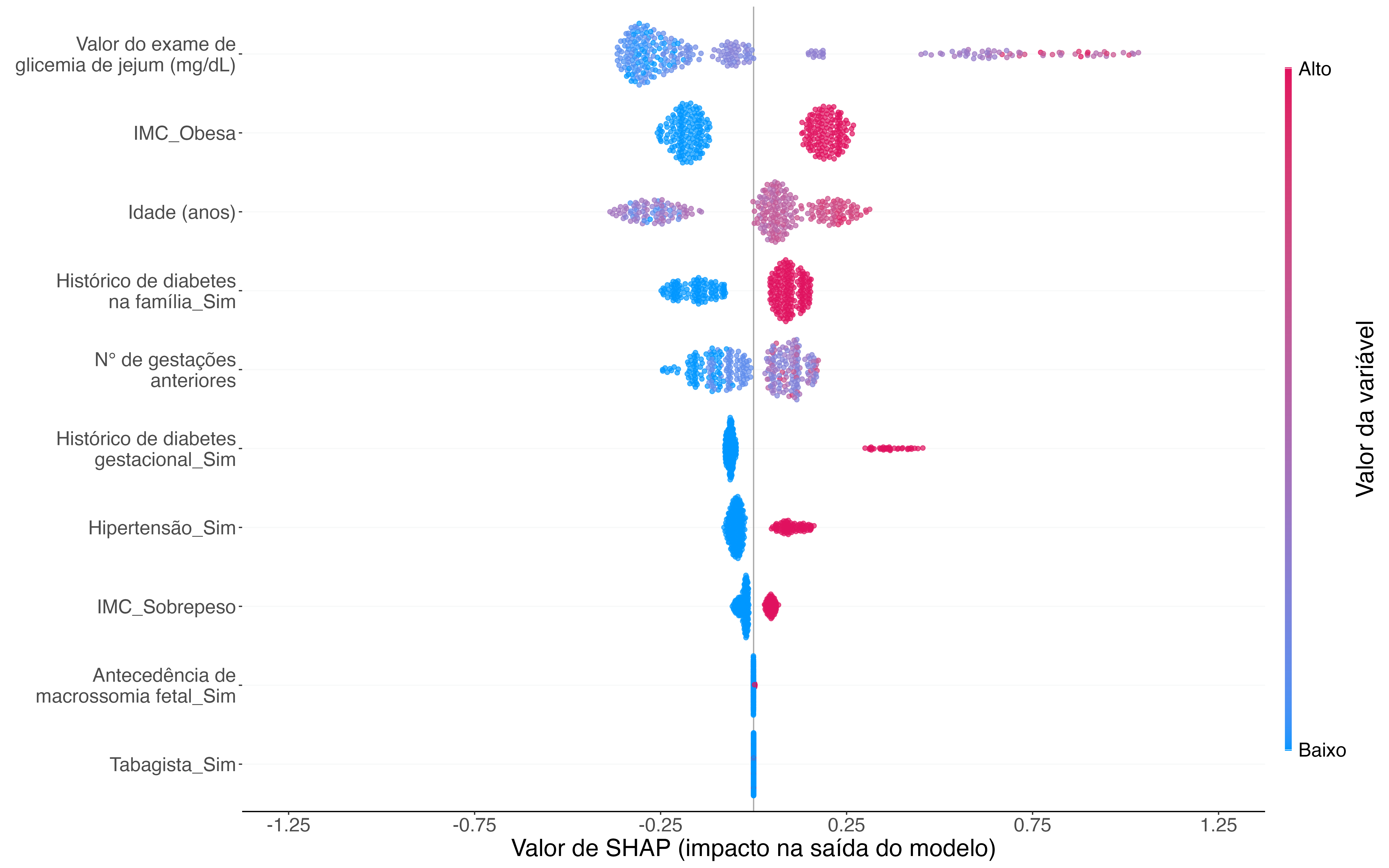
Figura 2: Gráfico de resumo SHAP para dados de diabetes gestacional do HCFMUSP.

Antes de interpretar o gráfico de resumo da Figura 2, vale um adendo: para o SHAP ser aplicável a covariáveis categóricas, elas precisam estar no formato dummy (ou seja, cada categoria da covariável vira 0 ou 1); logo, nessa situação, um “valor maior” e um “valor menor” acontecem quando o indivíduo é, respectivamente, 1 e 0 na categoria de tal covariável.

No gráfico de resumo gerado, além de identificarmos, mais uma vez, que o valor do exame de glicemia de jejum, a obesidade e a idade foram as covariáveis mais importantes, também podemos perceber que valores baixos nessas covariáveis têm valores de SHAP negativos (os pontos se alongam razoavelmente à esquerda com tons azuis) e valores altos nessas covariáveis têm valores de SHAP positivos (os pontos se desenvolvem à direita de zero com tons vermelhos e, no caso do valor de exame de glicemia de jejum, arroxeados). Na prática, isso significa que gestantes diagnosticadas com diabetes gestacional que atingiram altos valores de glicemia em jejum (possivelmente, maior do que 99 mg/dL), eram obesas e tinham idade mais avançada precisaram usar insulina em um momento precedente ao parto. Comportamento semelhante pode ser visto nas cinco covariáveis que seguem: ter histórico de diabetes na família, ter tido um maior número de gestações, ter histórico de diabetes gestacional, ser hipertensa e ter sobrepeso foram fatores que influenciaram no uso da insulina. Por outro lado, as covariáveis antecedência de macrossomia fetal (categoria: “sim”) e tabagista (categoria: “sim”), cujos valores de SHAP foram praticamente zero, não tiveram qualquer relevância nas classificações do modelo.

Gráfico de dependência SHAP

Como o leitor pode ter percebido, o gráfico de resumo oferece, tudo junto e misturado, uma gama de informações da relação dos valores de SHAP com as covariáveis. No entanto, para se ter ideia da verdadeira relação entre os valores de SHAP e uma covariável específica, o gráfico de dependência SHAP pode ser uma escolha mais interessante.

Quando as covariáveis são numéricas, os gráficos de dependência são semelhantes aos gráficos de dispersão, isto é, cada observação do conjunto de dados é representado por um ponto e a relação entre os valores de SHAP (eixo y) e uma covariável de interesse (eixo x) é vista por meio da dispersão desses pontos. Por isso, sua interpretação também é análoga aos gráficos de correlação: uma dada covariável pode ter relação linear positiva ou negativa, apresentar relação não linear ou ainda não ter qualquer relação com os valores de SHAP. Porém, quando lidamos com covariáveis do tipo categórica, o gráfico de dependência não traz nenhuma interpretação além da já apresentada pelo gráfico de resumo. Além disso, se traçamos uma linha horizontal na posição  y=0

“>y=0

, facilmente identificamos os pontos que obtiveram contribuições positivas (valores de SHAP acima de zero) e negativas (valores de SHAP abaixo de zero), assim como o ponto de corte no qual o modelo altera sua predição. Por fim, tenha cuidado ao fazer interpretações em regiões onde há poucos dados e, ao analisar vários gráficos de dependência ao mesmo tempo, prefira utilizar a mesma escala no eixo y (pois, assim, a influência que cada covariável tem sobre a predição do modelo é facilmente distinguida e seguramente comparável). Vejamos os três gráficos de dependência SHAP expostos na Figura 3, para os quais optamos por selecionar as três covariáveis mais influentes nas decisões do nosso modelo de predição XGBoost: valor do exame de glicemia de jejum, obesidade e idade.

Figura 3: Gráficos de dependência SHAP para dados de diabetes gestacional do HCFMUSP.

Para valor do exame de glicemia de jejum, observamos que valores abaixo de 100 mg/dL (nível de glicemia considerado normal) ocasionam valores de SHAP negativos, enquanto valores acima de 99 mg/dL determinam valores de SHAP positivos. Para idade, os valores de SHAP permanecem moderamente constantes abaixo de zero entre 15 e 30 anos de idade e aumentam acentuadamente acima de zero em idades superiores a 30 anos. Por último, notavelmente, gestantes obesas são mais suscetíveis a usar insulina antes do parto em comparação com aquelas que não o são.

Embora não tenha ocorrido em nossos dados, é importante mencionar que uma evidente dispersão vertical dos pontos em um valor específico de uma covariável configura efeito de interação com outras covariáveis. De outra forma, o que queremos dizer é que o valor de SHAP calculado para uma observação em uma certa covariável não é afetado apenas pelo valor dessa covariável em si, mas ele também é impactado pelos valores registrados dessa observação em outras covariáveis. Para exemplificar o que acabamos de dizer, avaliamos a possível interação entre valor do exame de glicemia de jejum e IMC classificado como obesa (Figura 4).

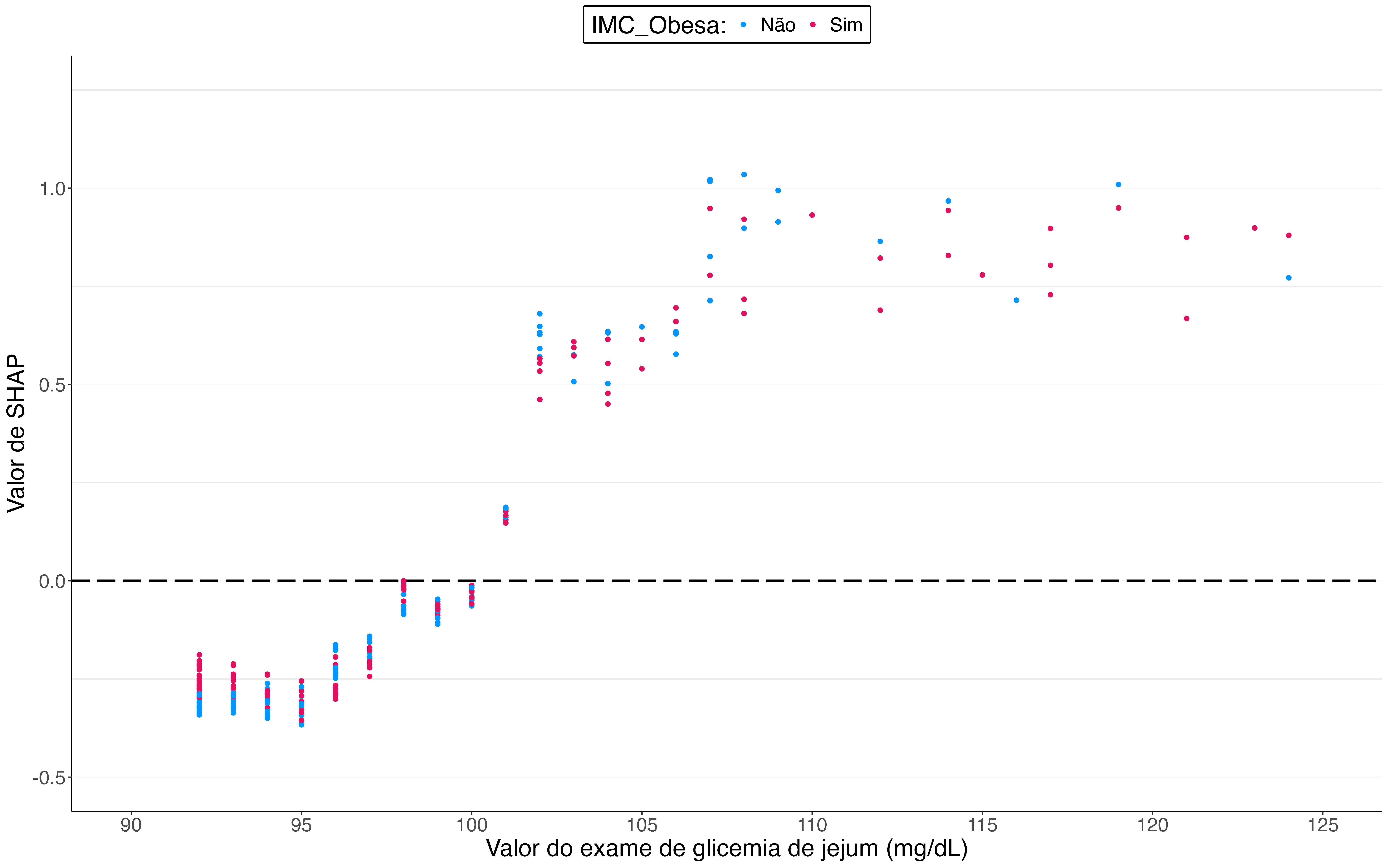
Figura 4: Gráfico de dependência SHAP com interação para dados de diabetes gestacional do HCFMUSP.

A interação entre as duas covariáveis não trouxe conclusões claras, ainda que gestantes diagnosticadas com diabetes gestacional e obesas pareceram estar mais associadas a valores de glicemia em jejum acima de 100 mg/dL e, portanto, mais sujeitas a usar insulina antes de realizarem o parto.

Obs.: um método de interpretabilidade global interessante para identificar possíveis interações entre covariáveis é o Interação das Covariáveis, que você também pode ver em Molnar (2020)[4].

Interpretabilidade individual (local)

Como vimos até aqui, métodos de interpretabilidade global geram interpretações baseadas em resultados médios das predições. Mas nem sempre uma mesma explicação é válida para todas as observações do nosso conjunto de dados, levando-nos a recorrer a métodos de interpretabilidade individual (ou local), que explicam a predição feita para uma única observação. No SHAP, as interpretações individuais, obtidas a partir das contribuições de cada uma das covariáveis de entrada do modelo, podem ser analisadas nos gráficos de cascata e de força.

Gráfico de cascata SHAP

Sua estrutura em cascata evidencia a natureza aditiva das covariáveis e como elas se baseiam no valor de base  (E[f(X)]) para gerar a predição  (f(x)) de uma observação específica.

Ao leitor, atenção! O valor de base é o mesmo para todas as observações dos dados, pois representa, em termos de valores de SHAP, a média da variável de desfecho (em modelos de regressão) ou a probabilidade média da categoria de interesse da variável de desfecho (em modelos de classificação) sem considerar quaisquer covariáveis – adaptando para o nosso problema, o valor de base é a probabilidade média de gestantes diagnosticadas com diabetes gestacional usar insulina antes do parto. Já o valor da predição ƒ(x) nada mais é do que os valores de SHAP calculados para uma observação somados ao valor de base.

Em um gráfico de cascata SHAP, as covariáveis, com seus respectivos valores de entrada, ficam dispostas no eixo y e os valores de SHAP, no eixo x. Os valores de SHAP, que denotam a quantidade e a direção que cada covariável assume no valor predito final, são vistos dentro de setas, que são vermelhas quando contribuem para a ocorrência do desfecho e azuis, caso contrário.

Para uma gestante qualquer do nosso estudo, geramos o gráfico de cascata que segue na Figura 5.

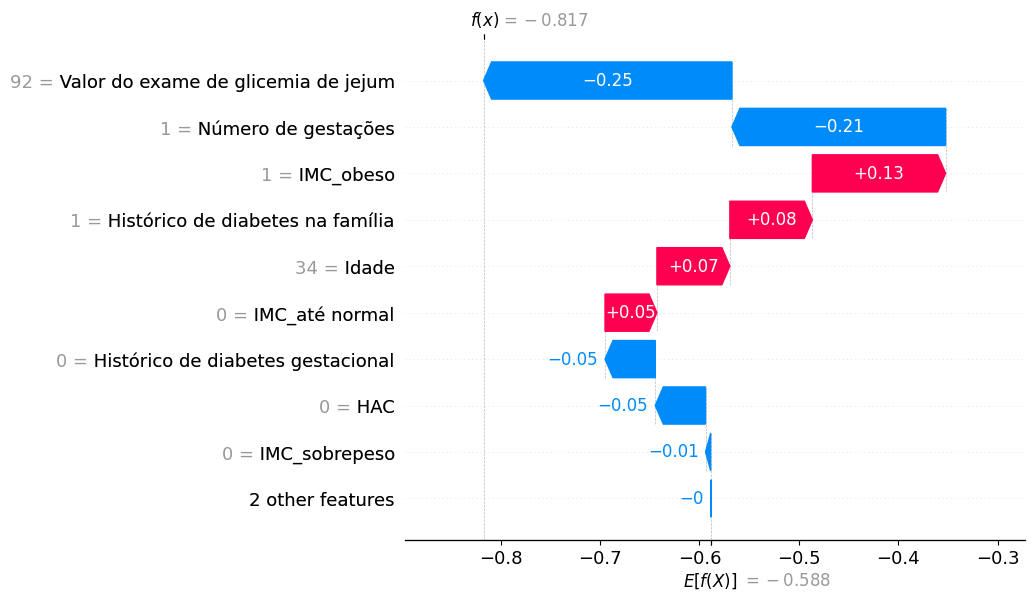
Figura 5: Gráfico de cascata SHAP para dados de diabetes gestacional do HCFMUSP.

Fatores como glicemia de jejum abaixo de 100 mg/dL, apenas uma gestação anterior e ausências de história de diabetes gestacional e hipertensão (HAC) diminuíram a chance de usar insulina antes do parto, ao passo que a obesidade e o histórico de diabetes na família causaram efeito contrário. Contudo, devido o resultado negativo de  ƒ(x),  a combinação dessas covariáveis e valores contribuíram para o prognóstico positivo para essa gestante em particular.

Gráfico de força SHAP

Uma outra opção, digamos, bastante atraente, para interpretar localmente as predições tomadas pelo seu modelo é o gráfico de força SHAP.

Semelhante ao gráfico de cascata, no gráfico de força também é apresentado como as covariáveis contribuem para “empurrar” o valor da predição ƒ(x) para longe do valor médio de todas as predições (que, lembrando, é o valor de base). As covariáveis que têm mais impacto na predição estão localizadas mais próximas da fronteira que divide as covariáveis que contribuíram positivamente (barras vermelhas e valores de SHAP positivos) e negativamente (barras azuis e valores de SHAP negativos). A magnitude das contribuições é quantificada pelo comprimento das barras.

Tomemos uma nova gestante, agora com características distintas daquela vista anteriormente.

Figura 6: Gráfico de força SHAP para dados de diabetes gestacional do HCFMUSP.

Pela Figura 6, fica claro que as covariáveis que mais contribuíram para a predição foram histórico familiar de diabetes (categoria: “0- não”), pelo lado negativo, e IMC classificado como obesa (categoria: “1- sim”), pelo lado positivo. E mais ainda, que não ter histórico de diabetes gestacional e familiar, ter tido uma única gestação, o valor de exame de glicemia de jejum estar avaliado em 100 mg/dL e não ser hipertensa foram fatores preponderantes para a desnecessidade da insulina antes do parto, embora a obesidade e a idade superior a 30 anos dessa gestante.

Obs.: note que as explicações dadas tanto pelo gráfico de cascata quanto pelo gráfico de força estão em consonância com as interpretações globais feitas antecedentemente.

Conclusão

No decorrer deste post, apresentamos o conceito principal do SHAP e como sua teoria robusta faz desse método um dos mais utilizados na área de aprendizado de máquina para interpretar, de forma global e individual, as decisões tomadas pelos modelos caixa-preta. Por meio de uma aplicação com dados reais, destrinchamos seus principais gráficos e explicamos minuciosamente como interpretá-los em um contexto de classificação – se a variável de desfecho é numérica, as interpretações são ainda mais fáceis. Do ponto de vista estatístico e clínico, ainda que suas interpretações não se tratem, necessariamente, de relações causais no mundo real, mostramos como o SHAP pode ser bastante útil para entender facilmente a relação entre um dado fator e desfecho sem abrir mão de um modelo com alto poder preditivo (no nosso caso, o XGBoost). Poder dizer que um modelo é confiável e justo a ponto de usá-lo na tomada de decisão, em vez de simplesmente fazê-la com base em predições às cegas, é primordial, se não vital, para a área da saúde.

Para dúvidas, comentários ou sugestões, escreva-nos em observatorioobstetricobr@gmail.com ou no nosso Instagram.

Referências

[1] da Fonseca, E. B., Bittar, R. E., Carvalho, M. H., & Zugaib, M. (2003). Prophylactic administration of progesterone by vaginal suppository to reduce the incidence of spontaneous preterm birth in women at increased risk: a randomized placebo-controlled double-blind study. American journal of obstetrics and gynecology, 188(2), 419-424.

[2] Romero, R., Nicolaides, K., Conde-Agudelo, A., Tabor, A., O’Brien, J. M., Cetingoz, E., … & Soma-Pillay, P. (2012). Vaginal progesterone in women with an asymptomatic sonographic short cervix in the midtrimester decreases preterm delivery and neonatal morbidity: a systematic review and metaanalysis of individual patient data. American journal of obstetrics and gynecology, 206(2), 124-e1.

[3] Souza, A. C., Costa, R. A., Paganoti, C. F., Rodrigues, A. S., Zugaib, M., Hadar, E., Moshe, H. & Francisco, R. P. (2019). Can we stratify the risk for insulin need in women diagnosed early with gestational diabetes by fasting blood glucose?. The Journal of Maternal-Fetal & Neonatal Medicine, 32(12), 2036-2041.

[4] Molnar, C. (2020). Interpretable machine learning. Lulu. com.

[5] Shapley, L. S. (2016). 17. A value for n-person games. Princeton University Press.

[6] Lundberg, S. M. & Lee, S.-I. (2017). A unified approach to interpreting model predictions. In Proceedings of the 31st international conference on neural information processing systems, pages 4768–4777.

[7] Izbicki, R., & dos Santos, T. M. (2020). Aprendizado de máquina: uma abordagem estatística. Rafael Izbicki.